Math 8 Kolaborasi

 Matematika

Kelas VIII

Bangun Ruang Sisi Datar

Membedakan dan menentukan luas permukaan dan volume bangun ruang sisi datar (kubus, balok, prisma, dan limas)

Assalamu'alaikum Wr. Wb.

Selamat pagi sholeh sholehah! Bagaimana kabarnya hari ini?
Semoga kita selalu dalam keadaan sehat walafiat. Aamiin.
Alhamdulillah hari ini kita bisa bertemu kembali dalam pelajaran Matematika. 

Walaupun dirumah saja selalu jaga kesehatan, cuci tangan dengan sabun dan jangan lupa beribadah kepada Alloh SWT.

Sudah melaksanakan shalat dhuha kah? semoga kita selalu istiqomah dalam menjalankan sholat dhuha dan sholat lima waktunya ya.

Sebelum memulai pembelajaran mari bersama-sama kita berdoa terlebih dahulu.

Tujuan pembelajaran pada pertemuan hari ini adalah dapat 

Menentukan luas permukaan dan volume kubus dan balok dengan menggunakan alat peraga berupa benda nyata.

Kubus

Pengertian Kubus

Kubus merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh enam sisi serupa yang berwujud bujur sangkar.

Kubus juga dikenal dengan nama lain yaitu bidang enam beraturan. Kubus sebetulnya adalah bentuk khusus dari prisma segiempat, sebab tingginya sama dengan sisi alas.

Bagian-bagian Kubus

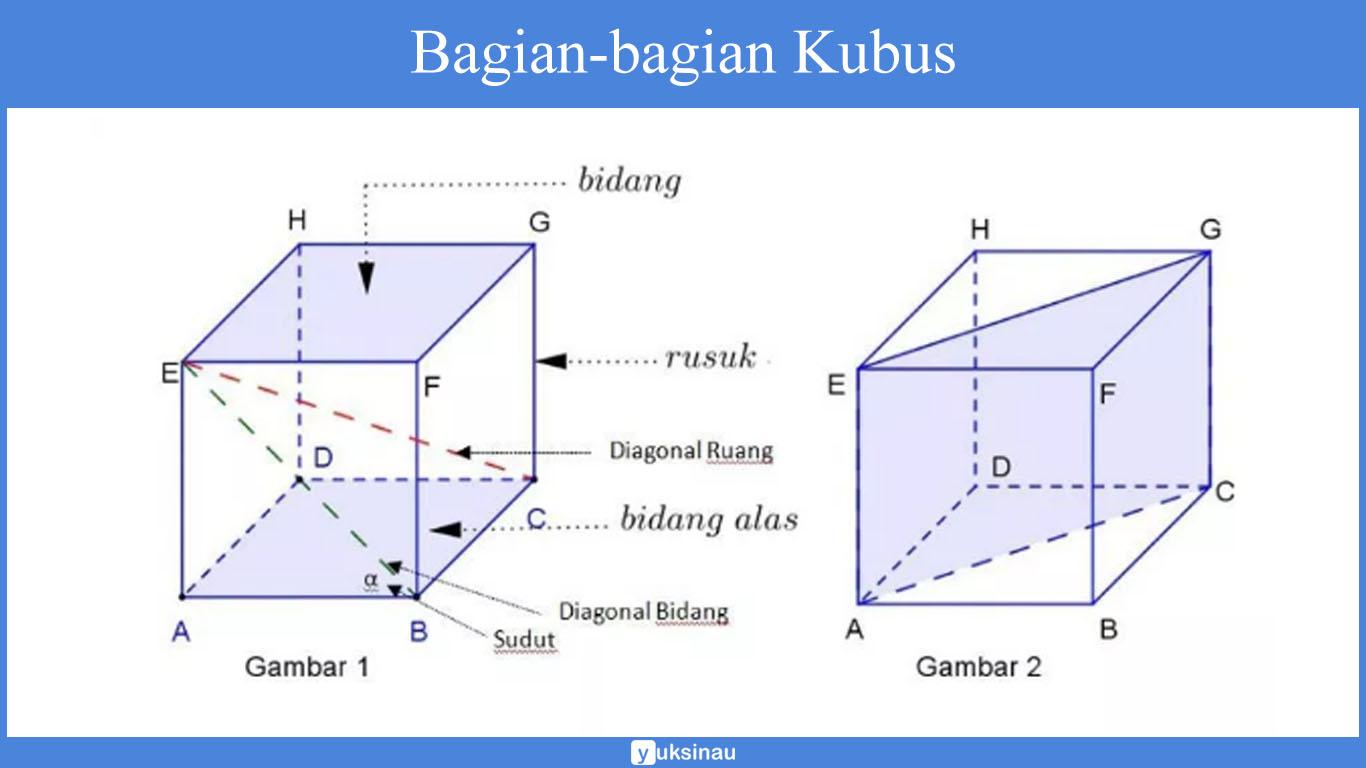
1. Sisi kongruen ada sebanyak 6 buah yang terdiri atas:
   • bidang alas kubus: ABCD
   • bidang atas kubus: EFGH
   • sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG.
2. Rusuk sama panjang ada sebanyak 12 buah (AB = BC = CD = DA = EF = FG = GH = HE = AE = BF = CG = DH).
3. Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
4. Diagonal bidang yang sama panjang sebanyak 6 buah (AC = BD = EG = FH = AF = BE = CH = DG = AH = DE = BG = CF).
5. Diagonal ruang yang sama panjang sebanyak 4 buah (AG = BH = CE =  DF).
6. Bidang diagonal kongruen berjumlah 6 buah (ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC).

Sifat bangun Kubus

1. Seluruh sisi kubus berbentuk persegi dengan mempunyai luas yang sama.
2. Seluruh rusuk kubus memiliki panjang yang sama.
3. Masing-masing diagonal bidang pada kubus mempunyai panjang yang sama.
   Perhatikan ruas garis BG dan CF pada gambar di atas. Kedua garis tersebut adalah diagonal bidang kubus ABCD.EFGH yang mempunyai ukuran sama panjang.
4. Masing-masing diagonal ruang pada kubus memiliki panjang yang sama.
   Dari kubus ABCD.EFGH pada gambar di atas , ada dua diagonal ruang, yakni HB dan DF di mana keduanya berukuran sama panjang.
5. Masing-masing bidang diagonal pada kubus berbentuk persegi panjang.
   Perhatikan bidang diagonal ACGE pada gambar di atas.

Jaring Jaring Kubus

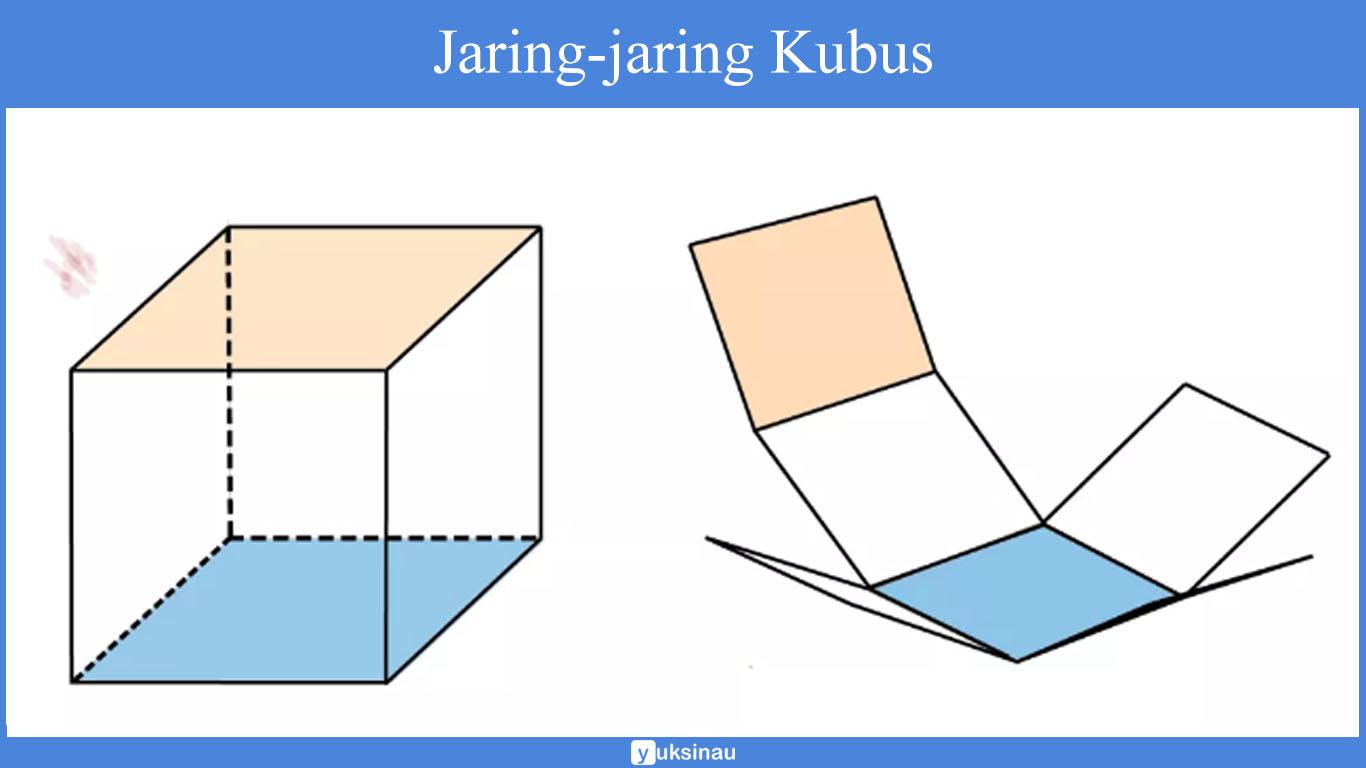
Jika kubus dipotong berdasarkan rusuk-rusuknya, lalu masing-masing sisinya direntangkan maka akan menghasilkan suatu bangun datar yang disebut sebagai jaring-jaring kubus.

Terdapat sebelas macam jaring-jaring kubus di mana susunannya berbeda satu sama lain. Masing-masing terdiri atas enam buah persegi kongruen yang saling berkaitan.

Simak gambar yang ada di bawah ini:

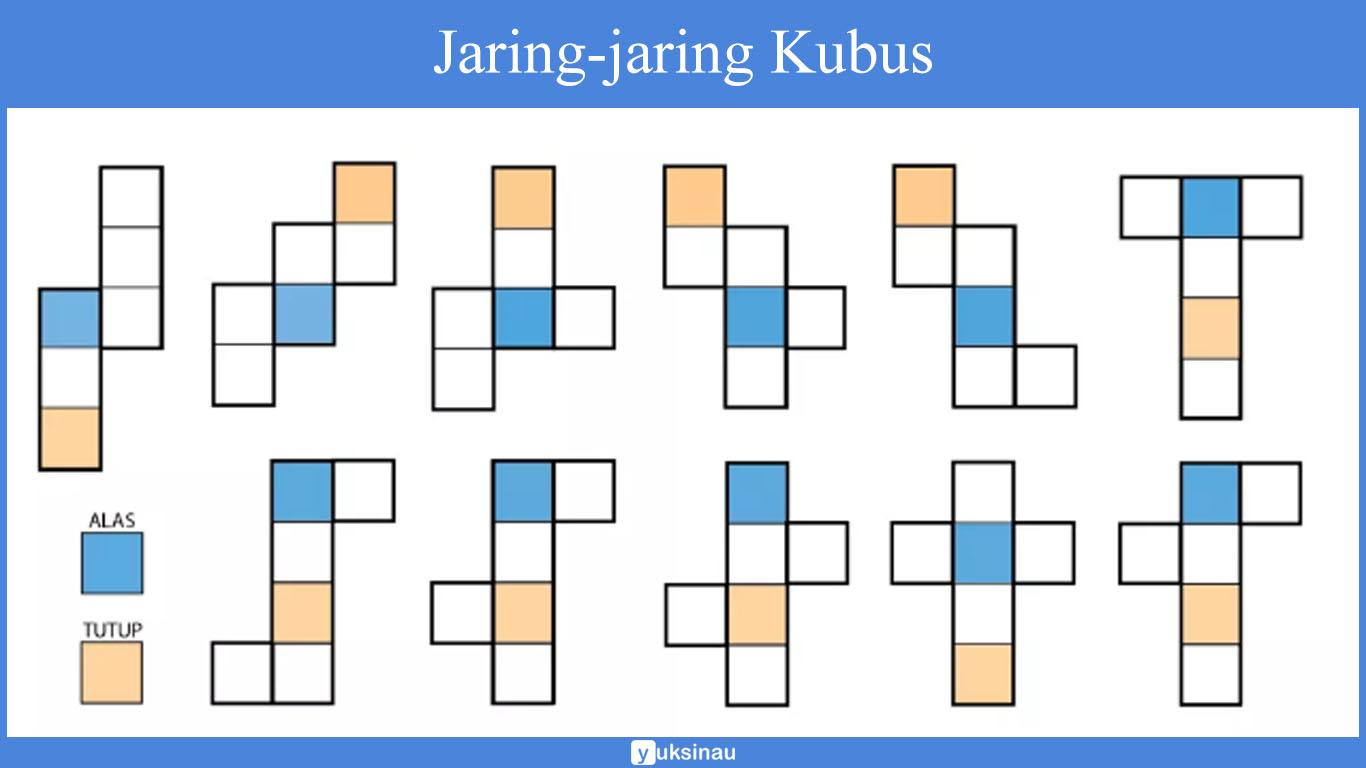
Rumus Pada Kubus

Volume: s x s x s = s3
Luas permukaan: 6 s x s = 6 s2
Panjang diagonal bidang: s√2
Panjang diagonal ruang: s√3
Luas bidang diagonal: s2√2

Contoh;

Diketahui sebuah bangun ruang kubus dengan panjang sisi sebuah kubus sebesar 20 cm, maka hitunglah Volume dan Luas permukaan Kubus tersebut.

Penyelesaian;

Rumus Volume Kubus : V = s³

Jadi Vol = 20 x 20 x 20

Volume = 8000 m³

Rumus Luas Permukaan Kubus : L = 6 x s²

L = 6 x 20 x 20

L = 2400 cm²

Balok

Pengertian Balok

Balok adalah suatu bangun ruang yang mempunyai tiga pasang sisi segi empat. Di mana pada masing-masing sisinya yang berhadapan mempunyai bentuk serta ukuran yang sama.

Berbeda halnya dengan kubus di mana seluruh sisinya kongruen berbentuk persegi, dan pada balok hanya sisi yang berhadapan yang sama besar.

Serta tidak seluruhnya berbentuk persegi, kebanyakan berbentuk persegi panjang.

Bagian Bagian Balok

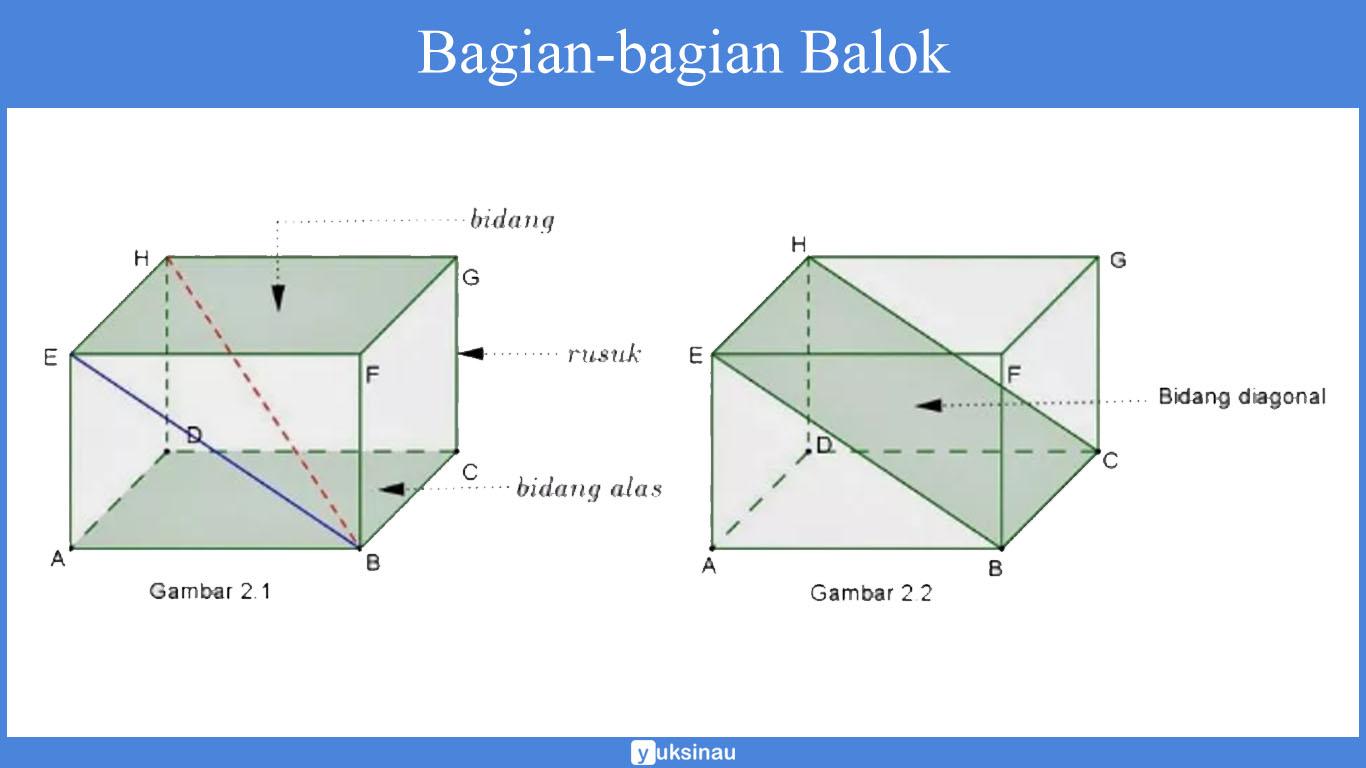
Pada masing-masing dari bangun ruang sisi datar yang satu ini sama seperti yang ada pada kubus.

Suatu balok terdiri tas sisi, sudut, diagonal bidang, diagonal ruang, serta yang terakhir yaitu bidang diagonal.

Berikut akan kami berikan rincian jumlahnya untuk kalian semua:

1. Sisi berbentuk persegi dan juga persegi panjang sebanyak 6 buah, antara lain yaitu:
   • bidang alas kubus: ABCD
   • bidang atas kubus: EFGH
   • sisi tegak kubus: ABEF, CDGH, ADEH, dan BCFG.
2. Rusuk sebanyak 12 buah yang dapat dibagi menjadi 3 kelompok, antara lain:
   • panjang (p) yakni rusuk terpanjang dari alas balok serta rusuk lainnya yang sejajar: AB, DC, EF dan HG
   • lebar (l) adalah rusuk terpendek dari alas balok dan juga rusuk lainnya yang sejajar: BC, AD, FG, dan EH
   • tinggi (t) adalah rusuk yang tegak lurus terhadap panjang dan lebar balok: AE, BF, CG, dan DH.
3. Titik sudut berjumlah 8 titik (A, B, C, D, E, F, G, H).
4. Diagonal bidang sebanyak 6 buah (AC, BD, EG, FH, AF, BE, CH, DG, AH, DE, BG, dan CF).
5. Diagonal ruang yang berjumlah 4 buah (AG, BH, CE, dan DF).
6. Bidang diagonal yang berbentuk persegi panjang dengan jumlah 6 buah, antara lain: ABGH, EFCD, BCHE, FGDA, BFHG, dan AEGC.

Sifat Balok

1. Sedikitnya sebuah balok mempunyai dua pasang sisi yang berbentuk persegi panjang.
2. Rusuk-rusuk yang sejajar memiliki ukuran yang sama panjang:
   AB = CD = EF = GH, dan AE = BF = CG = DH.
3. Pada masing-masing diagonal bidang pada sisi yang berhadapan berukuran sama panjang, yakni:
   ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE yang mempunyai ukuran sama panjang.
4. Masing-masing diagonal ruang pada balok mempunyai ukuran sama panjang.
5. Masing-masing bidang diagonalnya berbentuk persegi panjang.

Jaring Jaring Balok

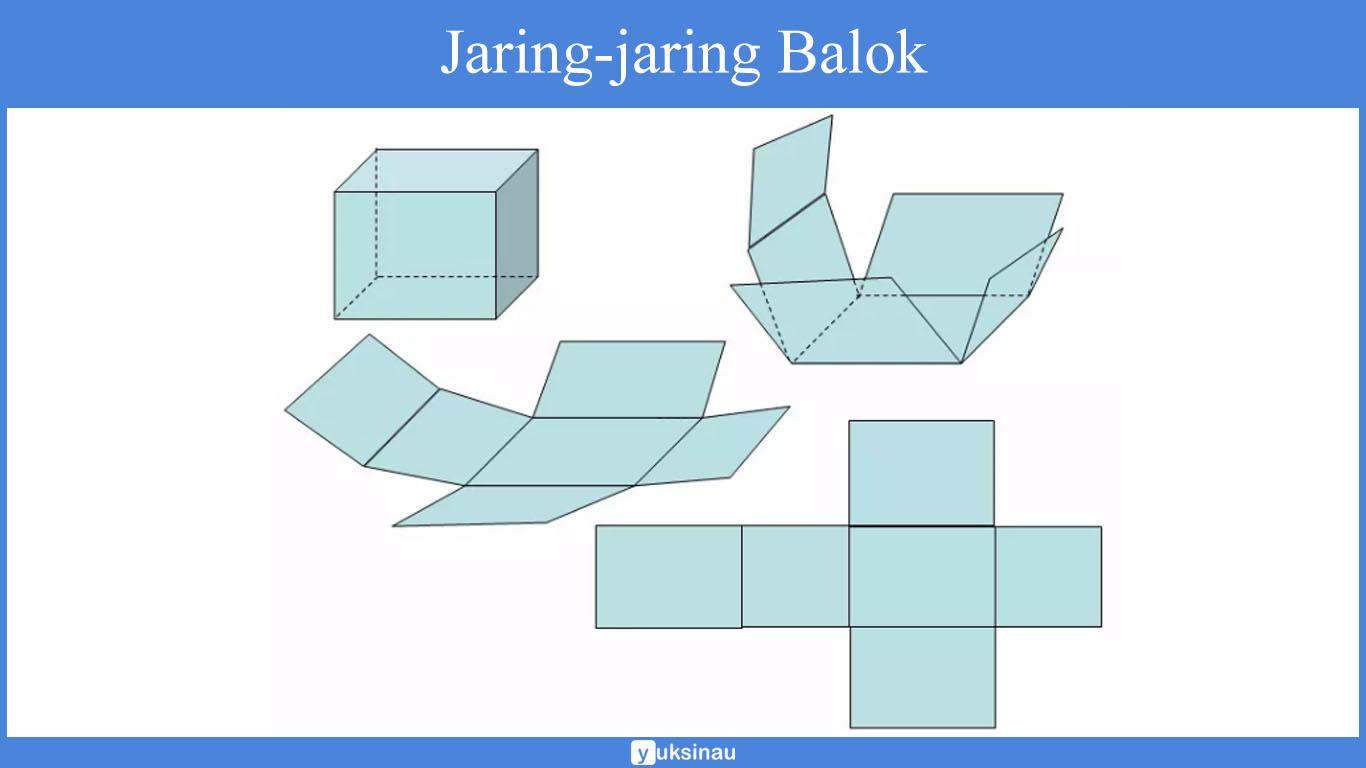
Sama halnya dengan kubus, jaring-jaring pada bangun balok juga didapatkan dengan cara membuka balok tersebut sehingga akan terlihat semua permukaan balok.

Coba kalian perhatikan baik-baik pada jalur pembuatan jaring-jaring balok di atas.

Jaring-jaring balok lebih banyak apabila dibandingkan dengan jaring-jaring pada kubus. Hal tersebut disebabkan selain persegi sisi-sisi pada balok juga terdiri atas persegi panjang.

Sehingga hasil  dari jaring-jaringnya menjadi lebih variatif.

Berikut adalah beberapa contoh dari jaring-jaring balok.

jaring

Rumus pada Balok:

Volume: p.l.t
Luas Permukaan: 2 (pl + pt + lt)
Panjang Diagonal Bidang: √(p2+l2) atau juga bisa √(p2+t2) atau √(l2+t2)
Panjang Diagonal Ruang: √(p2+l2+t2)

Keterangan:

p : panjang
l : lebar
t : tinggi

Contoh 1 

Sebuah balok mempunyai panjang 200 cm, lebar 10 cm dan tinggi 20 cm. Hitunglah luas dan volume balok tersebut.

JAWAB

Diketahui:
p = 200 cm
l = 10 cm
t = 20 cm

Volume balok:
V = p x l x t
V = (200) x (10) x (20)
V = 40.000 cm3

Luas balok
L = 2 x (p.l + p.t + l.t)
L = 2 x ((200)(10) + (200)(20) + (10)(20))
L = 2 x (6200)
L = 12400 cm2

Tugas!

Hitunglah luas permukaan dan volume balon terbang sederhana (kubus atau balok) dengan menggunakan alat peraga berupa benda nyata balon terbang sederhana pada tugas mata pelajaran IPA.

Kirimkan berupa video kolaborasi ke Wa ibu ya.

Terimakasih.

Sekian pembelajaran kita hari ini. Semoga menjadi ilmu yang bermanfaat untuk kita semua.

Tetap melaksanakan 3M semoga pandemi ini segera berakhir. Aamiin.

Waalaikumsalam Wr. Wb.