Math Kelas VII, VIII dan IX

Matematika

Kelas 7

Capaian Pembelajaran

Peserta didik dapat membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal, bilangan berpangkatbulat dan akar, bilangan dalam notasi ilmiah.

ATP

Peserta didik dapat membaca,menulis, dan membandingkan  bilangan rasional, bilangan desimal.

Setelah mempelajari operasi hitung pada bilangan pecahan sebelumnya mari kita menganalisis pemahaman dalam soal cerita berikut!

Ayo mencoba bersama kelompokmu

1. Ibu membeli tepung terigu sebanyak 2 kg. Tersebut akan dibuat menjadi beberapa kue, kata ibu khawatir tepung tersebut tidak cukup sehingga ibu membeli lagi sebanyak 1 ½kg.
   Untuk membuat kue nastar Ibu membutuhkan 1 ½ kg tepung terigu, untuk membuat kue bolu Ibu membutuhkan 1 ⅔kg, dan sisanya akan dibuat kue kacang. Berapakah berat tepung terigu yang digunakan untuk membuat kue kacang?
2. Tedy membutuhkan meter kain untuk membuat sebuah baju seragam. Jika Tedy ingin membuat 4 baju seragam, sedangkan Tedy hanya mempunyai 4 meter kain, paling sedikit berapa meter lagi yang harus dibeli Tedy?
3. Mili memiliki 3 botol susu yang masing-masing isinya liter. Susu tersebut akan dimasukkan ke dalam gelas. Setiap gelas berisi 1/5 liter. Berapa gelas yang akan dibutuhkan Mili?

Matematika 

Kelas VIII

Bidang Kartesius

3.2 Menjelaskan kedudukan titik dalam bidang koordinat Kartesius yang dihubungkan dengan masalah kontekstual

Tujuan pembelajaran pada pertemuan hari ini diharapkan peserta didik dapat menetukan jarak antar dua titik

Cara mencari jarak antar dua titik

Panjang garis ini dapat dicari menggunakan rumus jarak: √${\displaystyle (�2-�1{)}^2+(�2-�1{)}^2}$.

Langkah 1

Ambillah koordinat dari dua titik yang ingin Anda cari jaraknya. Sebutlah salah satu titik sebagai Titik 1 (x1,y1) dan titik lainnya sebagai Titik 2 (x2,y2).

• Misalnya, gunakan titik-titik (3,2) dan (7,8). Jika (3,2) adalah (x1,y1), maka (7,8) adalah (x2,y2).

Langkah 2

Ketahui rumus jarak. Rumus ini menghitung panjang garis yang terbentang di antara dua titik: Titik 1 dan Titik 2. Jarak liniernya merupakan akar kuadrat dari kuadrat jarak horizontal ditambah kuadrat jarak vertikal di antara kedua titik. Singkatnya, jarak linier merupakan akar kuadrat dari: 

Langkah 3

Carilah jarak horizontal dan vertikal di antara dua titik. Pertama, kurangkan y2 – y1 untuk mencari jarak vertikalnya. Kemudian, kurangkan x2 – x1 untuk mencari jarak horizontalnya. Jangan khawatir jika pengurangan menghasilkan angka negatif. 

• Carilah jarak yang searah dengan sumbu y. Untuk contoh titik-titik (3,2) dan (7,8), dengan (3,2) sebagai Titik 1 dan (7,8) sebagai Titik 2: (y2 – y1) = 8 -2 = 6. Ini berarti ada enam satuan jarak di antara kedua titik ini pada sumbu y.
• Carilah jarak yang searah dengan sumbu x. Untuk contoh titik-titik (3,2) dan (7,8): (x2 – x1) = 7 -3 = 4. Ini berarti ada empat satuan jarak yang memisahkan kedua titik itu pada sumbu x

 

Langkah 4

Kuadratkan kedua nilainya. Ini berarti Anda akan menguadratkan jarak pada sumbu x (x2 – x1), dan Anda akan menguadratkan jarak pada sumbu y (y2 – y1) secara terpisah

Langkah 5

Jumlahkan nilai kuadratnya. Penjumlahan ini akan menghasilkan kuadrat jarak linier diagonal di antara kedua titik Anda. Dalam contoh titik-titik (3,2) dan (7,8), kuadrat dari (7 – 3) adalah 16, dan kuadrat dari (8 – 2) adalah 36. 36 + 16 = 52.

Langkah 6

Carilah akar kuadrat dari persamaan. Ini adalah langkah terakhir dalam persamaan. Jarak linier di antara kedua titik merupakan akar kuadrat dari jumlah nilai kuadrat jarak pada sumbu x dan jarak pada sumbu y.

• Untuk melanjutkan contoh di atas: jarak antara (3,2) dan (7,8) adalah akar (52), atau sekitar 7,21 satuan.

Ayo Berlatih!

1. Dua buah titik A dan B berpisah dalam jarak d. Jika koordinat titik A(3,-2) dan B(-3,4), maka tentukanlah jarak antara titik A dan B.
2. Diketahui dua buah titik P(2,7) dan Q(8,3). Tentukanlah panjang garis PQ.

Matematika

Kelas IX

Persamaan Kuadrat

3.2       Menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya

Tujuan pembelajaran hari ini diharapkan peserta didik dapat meenganalisis faktor-faktor bentuk aljabar dalam persamaan kuadrat, penyelesaian (akar-akar) dari persamaan kuadrat, cara menentukan akar-akar persamaan kuadrat

Lanjutan pertemuan sebelumnya

Akar Persamaan Kuadrat Bentuk $a{x}^2+bx=0$

Untuk menentukan akar-akar persamaan kuadrat bentuk $a{x}^2+bx=0$, kita bisa mengubah bentuk persamaan kuadrat ini menjadi bentuk perkalian faktor-faktor aljabar dalam variabel $x$. Perhatikan berikut ini.

Dengan demikian, akar-akar persaman kuadrat bentuk $a{x}^2+bx=0$ adalah 0 dan $–b/\mathrm{a.}$

    Contoh:

    Dengan cara pemfaktoran, tentukanlah akar-akar dari persamaan berikut.

1. $4x^2-12x=0$

    Pembahasan:

1. Untuk $4x^2-12x=0$, maka


Dengan demikian, akar-akar dari $4x^2-12x=0$ adalah 0 atau 3.

Akar Persamaan Kuadrat Bentuk $x^2-c=0$

Untuk mencari akar-akar persamaan kuadrat bentuk $x^2-c=0$ kita bisa mengubahnya menjadi bentuk perkalian faktor-faktornya, yakni

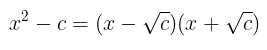
Dengan demikian, kita peroleh akar-akarnya yaitu $\sqrt{c}$ dan $-\sqrt{c}$.

     Contoh:

Tentukan akar-akar persamaan berikut dengan cara pemfaktoran.

1. $x^2-9=0$

    Pembahasan:

1. Untuk $x^2-9=0$, maka


Dengan demikian, akar-akar dari $x^2-9=0$ yaitu 3 dan -3.

          

       Ayo Berlatih!

      Tentukan akar-akar persamaan berikut dengan cara pemfaktoran.

1. $x^2+9x+14=0$
2. $x^2-36=0$
3. 
4. 3x² – 12x -12 = 0