Matematika
Kelas 7
Capaian Pembelajaran
Peserta didik dapat membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal, bilangan berpangkatbulat dan akar, bilangan dalam notasi ilmiah.
ATP
Peserta didik dapat membaca,menulis, dan membandingkan bilangan rasional, bilangan desimal.
Cara
Menyederhanakan Pecahan
·
Metode
1: Membagi pembilang dan penyebut dengan
bilangan bulat positif yang sama secara berulang-ulang sampai tidak dapat
dibagi lagi.
Contoh:
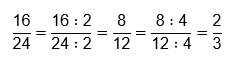
·
Metode
2: Bentuk sederhana dari bilangan
pecahan apabila FPB dari pembilang dan penyebutnya adalah 1. Jika FPB belum
sama dengan 1, cara menyederhanakannya adalah dengan membagi pembilang dan
penyebutnya dengan FPB tersebut.
Contoh:
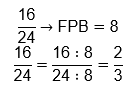
Cara
Membandingkan Pecahan
·
Metode
1: Untuk penyebut yang sama, hanya
membandingkan pembilangnya.
Contoh:

·
Metode
2: Untuk penyebut yang berbeda,
menyamakan penyebut terlebih dahulu lalu membandingkan pembilangnya. Cara
menyamakan penyebut:
o
Cara I: Mengalikan atau membagi pembilang dan penyebut dengan bilangan
bulat yang sama hingga penyebutnya sama.
o
Cara II: Penyebutnya sama-sama dibuat menjadi KPK dari penyebutnya.
Contoh:

·
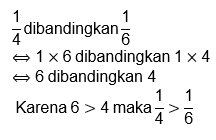
Metode Lain: Kali silang antara
pembilang dan penyebut.
Contoh:
Cara
Mengurutkan Pecahan
Menyamakan penyebut -> Mengurutkan pembilang.
Urutan pembilang = Urutan pecahan.
Contoh:

Soal
1. Tanda yang tepat untuk mengisi titik-titik di bawah ini adalah …
a. 2/4 … 3/5
b. 1/7 … 1/8
2. Sederhanakanlah pecahan 12/16!
3. Perhatikan pecahan berikut:
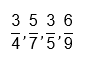
Urutan pecahan dari yang terkecil ke yang terbesar adalah…
Matematika
Kelas VIII
Bidang Kartesius
3.2 Menjelaskan kedudukan titik dalam
bidang koordinat Kartesius yang dihubungkan dengan masalah kontekstual
Tujuan pembelajaran pada pertemuan hari ini diharapkan peserta didik dapat mengidentifikasi konsep diagram kartesius dan mengidentifikasi pembagian kuadran bidang kartesius
Diagram Cartesius adalah sistem kordinat yang digunakan untuk meletakan titikpada penggambaran objek berdasarkan pemasukan nilai pada sumbu x dan nilai pada sumbu y dimana titik pertemuan ini nilai dari sumbu x dan sumbu y titik kordinat dibentuk. Jadi, diagram Cartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut. Di mana x disebut absis dan y disebut ordinat.
Titik-titik pada koordinat Cartesius merupakan pasangan titik pada sumbu-x dan sumbu-y (x, y). Perpotongan antara sumbu-x dan sumbu-y di titik 0 (nol) disebut pusat koordinat. Untuk bagian atas sumbu y bernilai positif, sedangkan pada bagian bawah sumbu y bernilai negatif. Begitu juga pada sebelah kanan sumbu x bernilai positif, sedangkan pada sebelah kiri sumbu x bernilai negatif.
Contoh:
Soal
Silahkan gambarkan titik-titik berikut pada bidang koordinat kartesius!
A (3, 4)
B (-4, 2)
C (-3, -2)
D (5, -3)


Tidak ada komentar:
Posting Komentar