Matematika
Kelas 8
Menjelaskan peluang empirik dan teoretik suatu kejadian
dari suatu percobaan
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait limas, peserta didik dapat memahami peluang empirik dari data luaran (output) yang mungkin
diperoleh dari sekelompok data.
Peluang
Percobaan
Percobaan adalah suatu tindakan atau kegiatan untuk memperoleh hasil tertentu. Percobaan disebut juga dengan eksperimen. Contoh percobaan antara lain melempar dadu, melempar uang koin, mengambil kartu secara acak dari tumpukan kartu, dan lain-lain.
Titik Sampel
Titik sampel adalah hasil dari percobaan. Misalnya, kita melakukan percobaan melempar satu buah dadu, maka titik sampelnya adalah (1), (2), (3), (4), (5), dan (6). Sementara itu, jika kita melakukan percobaan melempar satu buah uang koin, maka titik sampelnya adalah (A) dan (G). A berarti Angka dan G berarti Gambar.
Contoh lainnya, misalnya kita melemparkan dua buah uang koin, maka titik sampelnya adalah (A, A), (A, G), (G, A), dan (G, G).
Ruang Sampel
Ruang sampel adalah himpunan dari titik sampel. Ruang sampel juga biasa disebut dengan semesta dan disimbolkan dengan S. Ruang sampel berisi seluruh titik sampel yang ada, alias semua kemungkinan yang dapat muncul pada suatu percobaan.
Kita ambil contoh dari percobaan pada pembahasan titik sampel tadi. Percobaan pertama yaitu melempar satu buah dadu, dengan titik sampelnya adalah (1), (2), (3), (4), (5), dan (6). Maka, ruang sampelnya adalah S = {1, 2, 3, 4, 5, 6}.
Kemudian, percobaan kedua yaitu melempar satu buah uang koin, dengan titik sampelnya adalah (A) dan (G). Maka, ruang sampelnya adalah S = {A, G}.
Terakhir, percobaan ketiga yaitu melemparkan dua buah uang koin, dengan titik sampelnya adalah (A, A), (A, G), (G, A), dan (G, G). Maka, ruang sampelnya adalah S = {(A, A), (A, G), (G, A), (G, G)}.
Cara menyusun anggota ruang sampel ada 3:
1. Menyusun Anggota Ruang Sampel dengan Mendaftar
Cara pertama adalah menyusun anggota ruang sampel dengan mendaftar alias menuliskan seluruh anggota ruang sampel secara berurutan. Cara ini bisa dipilih ketika anggota ruang sampelnya tidak terlalu banyak.
Contohnya, saat kita melemparkan dua buah koin sekaligus, maka titik sampel atau semua hasil yang mungkin terjadi dari percobaan tersebut adalah (A, A), (A, G), (G, A), dan (G, G).
Maka, diperoleh ruang sampel:
S = {(A, A), (A, G), (G, A), (G, G)}
Banyak anggota ruang sampel → n(S) = 4
2. Menyusun Anggota Ruang Sampel dengan Diagram Pohon
Cara kedua adalah menyusun anggota ruang sampel dengan diagram pohon. Cara ini bisa dipilih ketika anggota ruang sampelnya cukup banyak dan akan memakan waktu jika menggunakan cara mendaftar.
Contohnya, saat kita melemparkan satu buah uang koin dan satu buah dadu, maka kemungkinan kejadiannya adalah munculnya angka (A) atau gambar (G) pada koin, dan salah satu mata dadu pada dadu.
Misalkan, uang koin dianggap bagian pertama, sementara dadu dianggap bagian kedua, maka bisa digambarkan diagram pohon sebagai berikut:
Maka, diperoleh ruang sampel:
S = {(A, 1), (A, 2), (A, 3), (A, 4), (A, 5), (A, 6), (G, 1), (G, 2), (G, 3), (G, 4), (G, 5), (G, 6)}
Banyak anggota ruang sampel → n(S) = 12
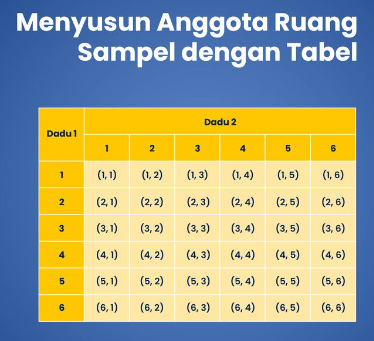
3. Menyusun Anggota Ruang Sampel dengan Tabel
Cara ketiga adalah menyusun anggota ruang sampel dengan tabel. Cara ini bisa dipilih ketika anggota ruang sampelnya sangat banyak dan akan memakan waktu jika menggunakan cara mendaftar maupun diagram pohon.
Contohnya, saat kita melemparkan dua buah dadu sekaligus, maka pada masing-masing dadu akan ada 6 kemungkinan kejadian yang muncul, yaitu mata dadu 1, 2, 3, 4, 5, dan 6. Jika kita susun dalam sebuah tabel, maka didapatkan hasil sebagai berikut:
Maka, diperoleh ruang sampel:
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Banyak anggota ruang sampel → n(S) = 36
Video
Peluang Empirik
https://www.youtube.com/watch?v=FnrT-hpGgkE
Ayo berlatih pada buku cetak halaman 283 nomor 12 tentang peluang empirik!