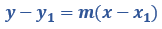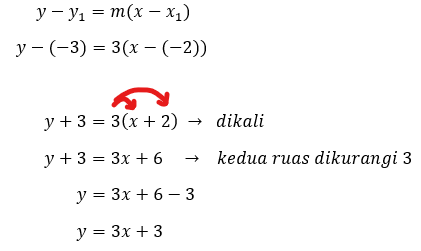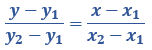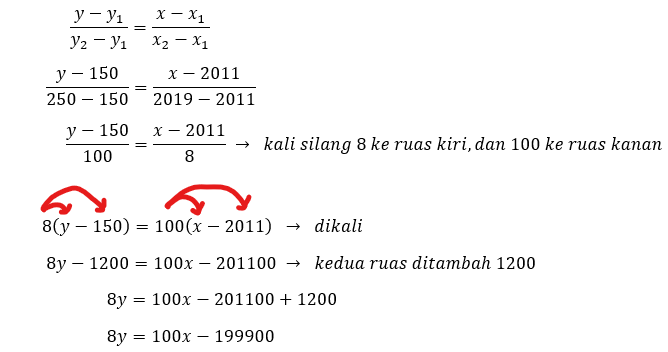Matematika
Kelas VII
Aljabar
Capaian Pembelajaran
Peserta didik dapat menggunakan pola dalam bentuk konfigurasi objek dan bilangan untuk membuat prediksi. Mereka dapat menemukan sifat-sifat komutatif, asosiatif, dan distributif operasi aritmetika pada himpunan bilangan real dengan menggunakan pengertian “sama dengan”, mengenali pola, dan menggeneralisasikannya dalam persamaan aljabar. Mereka dapat menggunakan “variabel” dalam menyelesaikan persamaan dan pertidaksamaan linear satu variabel. Mereka dapat menyajikan, menganalisis, dan menyelesaikan masalah dengan menggunakan relasi, fungsi linear, persamaan linear, gradien garis lurus di bidang koordinat Kartesius. Mereka dapat menyelesaikan sistem persaman linear dua variabel melalui beberapa cara. Mereka dapat menggunakan sifat-sifat operasi aritmetika dan “variabel” dalam menyelesaikan persamaan kuadrat dengan berberapa cara, termasuk faktorisasi dan melengkapkan kuadrat sempurna.
Alur Tujuan Pembelajaran :
1. Peserta didik mampu memahami arti huruf sebagai pengganti bilangan.
2. Peserta didik mampu menggunakan bentuk aljabar yang menggunakan huruf untuk memudahkan dalam menyelesaikan masalah.
Mengenal aljabar
Audio visual
https://youtu.be/lGPVGfBxcEw
Teks
A. Pengertian Bentuk Aljabar
Aljabar merupakan cabang ilmu matematika yang menggunakan tanda-tanda dan huruf-huruf untuk menggambarkan atau mewakili angka-angka (a, b, c, sebagai pengganti bilangan yang diketahui dan x, y, z untuk bilangan yang tidak diketahui). Besaran-besaran tersebut dinamakan variabel dan biasanya dilambangkan dengan huruf. Variabel adalah suatu besaran matematika yang nilainya dapat berubah (tidak konstan). Huruf-huruf dalam aljabar digunakan sebagai pengganti angka. Bentuk aljabar sering melibatkan angka (disebut konstanta), huruf (disebut perubah atau variabel), dan operasi hitung.
Lihatlah contoh di bawah ini:
3a berarti 3 x a atau (a + a + a)
a/3 berarti a : 3 atau 1/3 dari a
2ab berarti 2 x a x b atau (ab + ab)
a(-b) berarti a x a x (-b) atau –ab
(3a)2 berarti 3a x 3a atau 3 x a x 3 x a atau 32 x a2
a1/3 berarti 3√a
a2 – ¼ berarti (a x a – 1) : 4
B. Operasi Pemecahan Masalah Aljabar
Suatu ketika terjadi percakapan antara Pak Dzaki dan Pak Rayka. Mereka berdua baru saja membeli buku di suatu toko grosir.
Pak Dzaki : “Pak Rayka, kelihatannya beli buku tulis banyak sekali.”
Pak Rayka : “Iya, Pak. Ini pesanan dari sekolah saya. Saya beli 2 kardus dan 3 buku. Pak Dzaki beli apa saja?”
PakDzaki : “Saya hanya beli 5 buku Pak. Buku ini untuk anak saya yang kelas VII SMP.”
Dalam percakapan tersebut terlihat dua orang yang menyatakan banyak buku dengan satuan yang berbeda. Pak TRayka menyatakan jumlah buku dalam satuan kardus, sedangkan Pak Dzaki langsung menyebutkan banyak buku yang ia beli dalam satuan buku.

Simbol x tersebut bisa mewakili sebarang bilangan, yakni seperti berikut:
Jika x = 10, maka 2x + 3 = 2 × 10 + 3 = 20 + 3 = 23
Jika x = 15, maka 2x + 3 = 2 × 15 + 3 = 30 + 3 = 33
Jika x = 20, maka 2x + 3 = 2 × 20 + 3 = 40 + 3 = 43
Jika x = 40, maka 2x + 3 = 2 × 40 + 3 = 80 + 3 = 83
Jika x = 50, maka 2x + 3 = 2 × 50 + 3 = 100 + 3 = 103
Nilai pada bentuk aljabar di atas bergantung pada nilai x.
Di sekitar kita juga beberapa orang seringkali menyatakan banyaknya suatu benda tertentu dengan tidak menyebutkan satuan benda tersebut. Akan tetapi, mereka menggunakan satuan kumpulan dari jumlah benda tersebut. Misalkan satu karung beras, satu keranjang apel, satu keranjang jeruk, dan lain-lain.
Matematika
Kelas VIII
3.3 Mendeskripsikan
dan manyatakan relasi dan fungsi dengan menggunakan berbagai representasi
(kata-kata, tabel, grafik, diagram, dan persamaan)
Pada pertemuan hari ini bertujuan agar peserta didik dapat menjelaskan contoh kegiatan sehari-hari yang berkaitan
dengan relasi dan fungsi dan menjelaskan beberapa relasi yang terjadi diantara dua
himpunan
Relasi
1. Pengertian Relasi
Relasi ( hubungan ) dari himpunan A ke B adalah pemasangan anggota-anggota A dengan anggota-anggota B.
Relasi dalam matematika misalnya : lebih dari , kurang dari , setengah dari , faktor dari , dan sebagainya .
2. Menyatakan Relasi
Relasi antara dua himpunan dapat dinyatakan dengan 3 cara , yaitu : Diagram Panah , Diagram Cartesius , dan Himpunan pasangan berurutan .
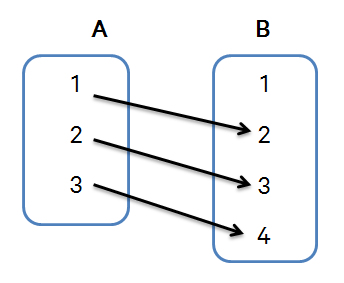
a. Diagram Panah
Contoh :
1. Jika Anto suka sepakbola , Andi suka voli dan bulutangkis serta Budi dan Badri suka
basket dan sepakbola . Buatlah Diagram Panah keadaan tersebut apabila A adalah
himpunan anak dan B adalah himpunan olahraga.
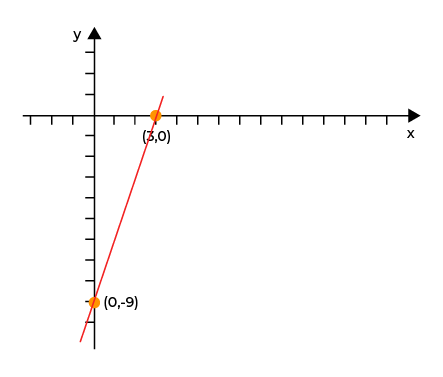
b. Diagram Cartesius
Contoh :
Diketahui A = { 1, 2, 3, 4, 5 } dan
B = { 1, 2, 3, …, 10 }.
Gambarlah diagram cartesius yang menyatakan relasi A ke B dengan
hubungan :
a. Akar kuadrat dari
C. Himpunan Pasangan Berurutan
Contoh :
Himpunan A = { 1, 2, 3, … , 25} dan
B = { 1, 2, 3, … , 10 } .
Tentukan himpunan pasangan berurutan yang menyatakan relasi A ke B dengan hubungan :
a. dua kali dari
b. satu kurangnya dari
Jawab:
a. { (2,1), (4,2), (6,3), (8,4), (10,5), (12,6),
(14,7),(16,8), (18,9),(20,10) }
b. { (1,2) , (2,3), (3,4), (4,5), (5,6), (6,7),
(7,8), (8,9), (9,10) }
Ayo Berlatih!
Diketahui P = {2, 4, 6} dan Q = {2, 3, 4}. Nyatakan relasi kedua himpunan diatas dengan:
- Himpunan pasangan berurutan dari P ke Q yang menyatakan "kelipatan dari“.
- Diagram panah P ke Q yang menyatakan "kelipatan dari“.