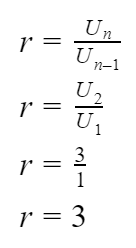Kamis, 31 Juli 2025

Math

Matematika

Kelas VII

Bilangan Bulat dan Pecahan

Pertemuan 6

 

Media/alat peraga: Laptob dan LCD, Buku matematika kelas VII

 

Capaian Pembelajaran

Membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal.

 

Tujuan Pembelajaran

Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan bilangan decimal

1.    - Bentuk baku

 

 

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

 

Ayo Simak Materi!

Bentuk baku, atau notasi ilmiah, adalah cara menulis bilangan yang sangat besar arau sangat kecil agar lebih mudah dibaca dan ditulis. Dalam bentuk baku, bilangan ditulis sebagai hasil kali dua faktor: faktor pertama adalah bilangan antara 1 dan 10 (termasuk 1), dan faktor kedua adalah perpangkatan dari 10. 

Ayo Simak Video!

https://www.youtube.com/watch?v=2UGBY4Z3TOA


Ayo Berlatih!

    1. Bentuk baku dari 125.000 adalah...

    2. Bentuk baku dari 0,0075 adalah...






    Matematika

    Kelas IX

    Bilangan Berpangkat dan Bentuk Akar

    Pertemuan 5


    Media/alat peraga: Laptob dan LCD


    Capaian Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. Bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.

    Tujuan Pembelajaran

    Peserta didik dapat menentukan bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.. 

    - pangkat pecahan dan bentuk akar


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Mari kita ingat kembali materi pada pertemuan sebelumnya tetang bilangan berpangkat positif, berpangkat negatif dan berpangkat nol. Hari ini kita akan mempelajari tentang bilangan berpangkat pecahan dan bentuk akar.

    Sifat-sifat bilangan berpangkat pecahan

    1. Perkalian Bilangan Berpangkat Pecahan

    Rumus atau bentuk umum untuk menghitung bilangan berpangkat pecahan adalah \[a^{\frac{m}{n}} \times a^{\frac{p}{q}} = a^{\frac{m}{n} + \frac{p}{q}}\]

    Contoh: \( 2^{\frac{1}{2}} \times 2^{\frac{1}{3}} = 2^{\frac{1}{2} + \frac{1}{3}} = 2^{\frac{3}{6} + \frac{2}{6}} = 2^{\frac{5}{6}} \)

    2. Pembagian Bilangan Berpangkat Pecahan

    Bentuk umum dari pembagian bilangan berpangkat pecahan yaitu \[\frac{a^{\frac{m}{n}}}{a^{\frac{p}{q}}} = a^{\frac{m}{n} - \frac{p}{q}}\]

    Contoh: \( \frac{3^{\frac{2}{3}}}{3^{\frac{1}{4}}} = 3^{\frac{2}{3} - \frac{1}{4}} = 3^{\frac{8}{12} - \frac{3}{12}} = 3^{\frac{5}{12}} \)

    3. Pangkat dari Pangkat Pecahan

    Sedangkan operasi bilangan berpangkat dari pangkat pecahan memiliki bentuk \[\left( a^{\frac{m}{n}} \right)^{\frac{p}{q}} = a^{\frac{m}{n} \times \frac{p}{q}}\]

    Contoh: \( \left( 5^{\frac{2}{3}} \right)^{\frac{3}{4}} = 5^{\frac{2}{3} \times \frac{3}{4}} = 5^{\frac{6}{12}} = 5^{\frac{1}{2}} \)

    Akar sebagai Pangkat Pecahan

    Sifat bilangan eksponen berpangkat selanjutnya memiliki bentuk umum seperti \[\sqrt[n]{a} = a^{\frac{1}{n}}\]

    Contoh: \( \sqrt[3]{8} = 8^{\frac{1}{3}} \)

    5. Pembalikan Pangkat Pecahan

    Terakhir, bilangan berpangkat memiliki sifat pembalikan pangkat pecahan dengan rumus atau bentuk umum \[a^{-\frac{m}{n}} = \frac{1}{a^{\frac{m}{n}}}\]

    Contoh: \( 4^{-\frac{1}{2}} = \frac{1}{4^{\frac{1}{2}}} = \frac{1}{2} \)

    Ayo simak video berikut:


    Ayo Berlatih!

    1. Jika 8^{\frac{2}{3}} = x, berapakah nilai x?
    2. Tentukan hasil dari 27^{\frac{1}{3}}!
    3. Nilai dari 16^{\frac{3}{4}} adalah…
    4. Jika 125^{\frac{2}{3}} adalah y, berapakah y?



    Diposting oleh di Tidak ada komentar:

    Rabu, 30 Juli 2025

    Math

     Matematika

    Kelas VIII

    Pola Bilangan

    Pertemuan 5


    Media/alat peraga: Laptob dan LCD

    Capaian Pembelajaran

    Memprediksi dan menggeneralisasi pola dalam bentuk susunan benda dan bilangan.

    Tujuan Pembelajaran

    Peserta didik dapat mengenali, memprediksi dan menggeneralisasi pola dalam  bentuk susunan benda(obyek) dan pola bilangan

    - Memprediksi pola barisan geometri


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Barisan geometri adalah pola yang memiliki pengali atau rasio yang tetap untuk setiap 2 suku yang berdekatan. Rasio pada barisan geometri biasa disimbolkan dengan r. Barisan geometri juga biasa disebut sebagai barisan ukur.

    Contoh lebih mudahnya begini, misal kamu punya barisan seperti ini:

    1, 3, 9, 27, …

     

    Dari barisan tersebut, kita bisa lihat antara suku pertama dengan suku kedua, antara suku kedua dan suku ketiga dan seterusnya selalu punya pengali yang tetap, yaitu 3. Dengan demikian, barisan ini termasuk barisan geometri.



    Contoh:

     barisan geometri:

    1, 3, 9, 27, 81, ….

    Suku pertama (a) dari barisan geometri tersebut adalah 1. Maka r-nya adalah:

    mtk 1

    Jadi, rasio dari barisan geometri tersebut adalah 3.


    Untuk mencari Un pada barisan geometri bisa menggunakan rumus berikut ini:


    Contoh:

     barisan geometri:

    1, 3, 9, 27, 81, ….

    Lalu, kita coba cari Un nya. Misalnya n yang mau dicari adalah 6, maka:

    Un = arn-1

    U6 = ar5

    U6 = 1 . 35

    U6 = 1 . 243

    U6 = 243

    Jadi, U6 dari barisan geometri tersebut adalah 243.



    Ayo Simak Video!


    Ayo Berlatih!
    1. Diberikan suatu barisan 3, 9, 27, 81...
    Tentukan:
    a. rasio dari barisan tersebut
    b. suku ke-10 dari barisan tersebut.




    Matematika

    Kelas VII

    Bilangan Bulat dan Pecahan

    Pertemuan 5

     

    Media/alat peraga: Laptob dan LCD, Buku matematika kelas VII

     

    Capaian Pembelajaran

    Membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal.

     

    Tujuan Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan bilangan decimal

    1.    - FPB dan KPK

     

     

    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

     

    Ayo Simak Materi!

    Kelipatan adalah mengalikan bilangan dengan setiap bilangan asli secara berurutan. Misalnya, kita pilih satu bilangan, yaitu 2. Kemudian, bilangan 2 tersebut kita kalikan dengan bilangan asli secara berurutan, seperti:

    2 × 1 = 2

    2 × 2 = 4

    2 × 3 = 6 … dst.

    Jadi, bilangan 2, 4, 6, dan seterusnya merupakan kelipatan dari 2.


    Faktor adalah bilangan-bilangan yang dapat membagi sampai habis suatu bilangan. Misalnya, kita pilih satu bilangan, yaitu 10. Nah, bilangan 10 ini kira-kira bisa habis dibagi oleh bilangan apa saja, nih? Benar! Bilangan 10 bisa dibagi oleh 1, 2, 5, dan 10. Jadi, 1, 2, 5, dan 10 ini merupakan faktor dari 10.

    Contoh:

    Kita akan menentukan KPK dari 2 bilangan, yaitu 5 dan 6. Langkah pertama yang kita lakukan adalah mencari kelipatan dari masing-masing bilangan tersebut.

    5 = 5, 10, 15, 20, 25, 30, …

    6 = 6, 12, 18, 24, 30, …

    Setelah itu, kita peroleh kelipatan bilangan terkecil yang sama dari 5 dan 6, yaitu 30. Jadi, KPK dari 5 dan 6 adalah 30.

    Contoh:

    Kita akan mencari nilai FPB dari 2 bilangan, yaitu 12 dan 18. Langkah pertama yang kita lakukan adalah mencari faktor atau bilangan yang dapat membagi habis dari masing-masing bilangan tersebut.

    12 = 1, 2, 3, 4, 6, 12.

    18 = 1, 2, 3, 6, 9, 18.

    Setelah itu, kita peroleh faktor bilangan terbesar yang sama dari 12 dan 18, yaitu 6. Jadi, FPB dari 12 dan 18 adalah 6.

    Contoh soal cerita

    Tiga orang satpam mendapat giliran jaga pada malam hari. Satpam pertama mendapat giliran tiap 2 hari sekali. Satpam kedua setiap 5 hari sekali, sedangkan satpam ketiga setiap 6 hari sekali. Jika tanggal 1 Desember 2000 semua bertugas bersama-sama pertama kali, maka mereka bertugas bersama-sama lagi untuk yang ketiga kali pada tanggal...


    Ayo Simak Video!

    https://www.youtube.com/watch?v=umyYLCWMzw0


    Ayo Berlatih!

    1. Bilangan kelipatan 4 antara 12 dan 36 adalah...
    2. Semua faktor dari 56 adalah...
    3. Firdha, Sabrina, dan Sekha menari di sanggar yang sama. Firdha berlatih setiap 6 hari sekali, Sabrina berlatih setiap 8 hari sekali, dan Sekha berlatih setiap 4 hari sekali. Jika pada tanggal 9 September 2013 mereka berlatih bersama-sama, maka mereka akan berlatih bersama-sama lagi untuk yang kedua kalinya pada tanggal...
    4. Ibu membeli 90 biskuit, 60 permen cokelat, dan 45 kaleng susu yang akan dikemas untuk acara ulang tahun Adik. Setiap kemasan berisi jenis dan jumlah barang yang sama. Kemasan terbanyak yang dapat dibuat adalah...



    Diposting oleh di Tidak ada komentar:

    Senin, 28 Juli 2025

    Math

    Matematika

    Kelas VIII

    Pola Bilangan

    Pertemuan 4


    Media/alat peraga: Laptob dan LCD

    Capaian Pembelajaran

    Memprediksi dan menggeneralisasi pola dalam bentuk susunan benda dan bilangan.

    Tujuan Pembelajaran

    Peserta didik dapat mengenali, memprediksi dan menggeneralisasi pola dalam  bentuk susunan benda(obyek) dan pola bilangan

    - Memprediksi pola deret aritmetika


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Deret aritmatika (Sn) adalah jumlah suku ke-n pada barisan aritmatika. Nah, di sini kita hanya menjumlahkan barisan aritmatikanya saja sampai ke suku yang diperintahkan.             Misalnya, kamu diperintahkan untuk mencari deret aritmatika jumlah 5 suku pertama dari barisan yang tadi dibahas. Jadi seperti ini ya penjelasannya.

    3, 7, 11, 15, 19, …

    Jumlah 5 suku pertamanya berarti,

    3 + 7 + 11 + 15 + 19 = 55




    Ayo Simak Video!


    Ayo Berlatih!

    1. Diketahui deret bilangan aritmatika sebagai berikut.

      12 + 15 + 18 + …

      Jumlah delapan suku pertama deret tersebut adalah…

    2. Diketahui deret aritmatika: 3 + 7 + 11 + 15 + …

      Jumlah 15 suku pertama deret tersebut adalah…





    Matematika

    Kelas IX

    Bilangan Berpangkat

    Pertemuan 4


    Media/alat peraga: Laptob dan LCD


    Capaian Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. Bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.

    Tujuan Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. 

    - Menyelesaikan soal bilangan berpangkat


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Mari kita ingat kembali materi pada pertemuan sebelumnya tetang bilangan berpangkat positif, berpangkat negatif dan berpangkat nol. Kita akan menyelesaikan soal-soal tapi sebelumnya mari kita simak video berikut:


    Kita berkonsentrasi dengan pancasila game untuk menentukan siapa saja yang akan mendapatkan soal pada kartu soal. setelah mendapatkan soal silahkan dikerjakan untuk mendapatkan poin. bagi yang menjawab kurang tepat maka soal tersebut dapat diberikan ke teman lain atau ke pembuat soal.





    Diposting oleh di Tidak ada komentar:

    Kamis, 24 Juli 2025

    Math

    Matematika

     

    Kelas VII

     

    Bilangan Bulat

     

    Pertemuan 4

     

    Media/alat peraga: Laptob dan LCD, Buku matematika kelas VII

     

    Capaian Pembelajaran

    Membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal.

     

    Tujuan Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan bilangan decimal

    1.    - Operasi campuran bilangan bulat

     

     

    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

     

    Ayo Simak Materi!

    Operasi campuran bilangan bulat adalah operasi hitung yang melibatkan lebih dari satu jenis operasi dasar (penjumlahan, pengurangan, perkalian, dan pembagian) pada bilangan bulat. Untuk menyelesaikannya, perlu diperhatikan urutan pengerjaan yang benar, yaitu: kurung, perkalian dan pembagian (dikerjakan dari kiri), dan penjumlahan dan pengurangan (dikerjakan dari kiri). 

    Contoh soal

    1. Hitunglah 

    10 + 2 × (-7)

    Jawab: 10 + 2 × (-7) = 10 + -14 = -4 

    2. Hitunglah berikut ini dengan sifat distributif. 
    (-6) × 55 + (-6) × 45
    Jawab: Sifat distributif digunakan untuk menyederhanakan suatu operasi hitung. Menurut sifat distributif, a x b + a x c = a x (b + c). Maka  -6) × 55 + (-6) × 45 = (-6) x (55 + 45) = (-6) x 100 = -600

    3. Hitungan dengan kombinasi empat operasi.
    4 × (-2) + (-14) : 2
    Jawab: 4 × (-2) + (-14) : 2 = (-8) + (-7) = -15


    Ayo Simak Video!

    https://www.youtube.com/watch?v=ZkQP1tvn8SE


    Ayo Berlatih!

    1. Kerjakan perhitungan (15 - 6) \times (4 + 2).
    2. Cobalah untuk menyelesaikan perhitungan (5 \times 2) + (7 \div 3).
    3. Selesaikan (27 \div 9) \times (4 + 1)!
    4. Hitung hasil dari (18 \times 3) \div 6 + (9 - 2).
    5. Cobalah hitung 24 \div (5 - 2) + (3 \times 4).




    Matematika

    Kelas IX

    Bilangan Berpangkat

    Pertemuan 3


    Media/alat peraga: Laptob dan LCD


    Capaian Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. Bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.

    Tujuan Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. 

    - Menyelesaikan soal bilangan berpangkat


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Mari kita ingat kembali materi pada pertemuan sebelumnya tetang bilangan berpangkat positif, berpangkat negatif dan berpangkat nol. Kita akan menyelesaikan soal-soal tapi sebelumnya mari kita simak video berikut:


    Silahkan masingmasing peserta didik membuat kartu soal yang akan kita share dan selesiakan dengan bertukar kartu dikelas nanti. Kita akan menyelesaikannya dengan permainan bersama.


    Diposting oleh di Tidak ada komentar:

    Rabu, 23 Juli 2025

    Math

    Matematika

    Kelas VIII

    Pola Bilangan

    Pertemuan 3


    Media/alat peraga: Laptob dan LCD

    Capaian Pembelajaran

    Memprediksi dan menggeneralisasi pola dalam bentuk susunan benda dan bilangan.

    Tujuan Pembelajaran

    Peserta didik dapat mengenali, memprediksi dan menggeneralisasi pola dalam  bentuk susunan benda(obyek) dan pola bilangan

    - Memprediksi pola barisan aritmetika


    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.



    Ayo simak materi!

    Pada pertemuan sebelumnya kita sudah mempelajari tentang jenis-jenis pola bilangan. Hari ini kita akan mengenal pola barisan aritmetika.

    Rumus barisan aritmetika bisa kamu gunakan untuk mencari suku ke-n (Un). Sementara itu, rumus deret aritmetika berguna untuk mencari penjumlahan dari suku-suku tersebut.

    Oke, supaya kamu lebih mudah memahami rumusnya, kita langsung masuk ke contoh soal saja. Misalnya terdapat barisan bilangan 1, 3, 5, 7, 9, 11, … Maka,

    Suku pertama = U1 = a = 1

    Suku kedua = U2 = 3

    Suku kedua = U3 = 5 … dst sampai suku ke-n = Un

    Beda atau selisih suku pertama dengan suku kedua, suku kedua dengan suku ketiga, dan seterusnya:

    b = U2 – U1 = 3 – 1 = 2

    b = U3 – U2 = 5 – 3 = 2

    b = U4 – U3 = 7 – 5 = 2 … dst

    Jadi, b = 2.

    Kita diminta mencari suku ke-n (Un) dari barisan bilangan tadi. Kalau semisal yang ditanya adalah suku ke-7 (U7), caranya gampang ya, gais. Kamu tinggal tambahkan saja suku ke-6 (U6) dengan nilai beda nya.

    b = U7 – U6

    U7 = U6 + b

    U7 = 11 + 2 = 13

    Tapi, bagaimana jika kita diminta untuk mencari suku ke-20, atau suku ke-35, atau suku ke-100? Sangat nggak efektif kalau kita jumlahkan satu per satu tiap suku dengan beda nya, ya. Oleh karena itu, kita membutuhkan rumus barisan aritmetika.

    Ayo Simak Video!

    Contoh soal 1

    1. Pada barisan aritmatika 7, 5, 3, 1, suku ke 20-nya adalah …

    Pembahasan:

    ·         Diketahui:

    a = 7

    b = U2 – U1

    b = 5-7

    b = –2

    ·         Rumus:

    Un = a + (n-1)b

    Un = 7 + (20-1) (-2)

    = 7 + (19).-2

    = 7 + (-38)

    = -31


    2. Rumus suku ke-n pada barisan bilangan 2, 6, 8, ...

    Pembahasan:

         Diketahui:

    a = 2

    b = 4 – 2

    b = 2


    ·         Rumus:

    Un = a + (n-1)b

    Un = 2 + (n-1)2

    Un = 2 + 2n -2

    Un = 2 - 2 + 2n

     Un = 2n


    Ayo Berlatih!
    1. pada suatu barisan aritmatika 10, 6, 2, -2, -6, -10. Berapakah beda barisan tersebut?
    2. Pada suatu ruangan rapat, disusun kursi dengan baris depan 12 kursi, baris kedua 14 kursi, baris ketiga 16 kursi. Maka banyaknya kursi di baris ke 5 adalah …
    3. Suatu barisan aritmatika adalah 2, 6, 10, … maka suku ke-14 adalah...
    4. Susun rumus suku ke-n pada barisan bilangan 4, 7, 10 …



    Matematika

     

    Kelas VII

     

    Bilangan Bulat

     

    Pertemuan 3

     

    Media/alat peraga: Laptob dan LCD, Buku matematika kelas VII

     

    Capaian Pembelajaran

    Membaca, menulis, dan membandingkan bilangan bulat, bilangan rasional dan irasional, bilangan desimal.

     

    Tujuan Pembelajaran

    Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan bilangan decimal

    1.    - Perkalian dan pembagian bilangan bulat

     

     

    Assalamualaikum Wr. Wb.

    Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
    Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

     

    Ayo Simak Materi!

    Sifat-sifat Operasi Perkalian Bilangan Bulat

    Apabila a adalah bilangan bulat positif, maka a>0. Namun, apabila a adalah bilangan bulat negatif, maka a<0. Berikut ini adalah sifat-sifat operasi perkalian bilangan bulat:

    1. Tertutup, jika a dan b adalah bilangan bulat, maka a x b akan menghasilkan bilangan bulat juga
    2. Komutatif (pertukaran) a x b = b x a
    3. Asosiatif (pengelompokkan) a x (b x c) = (a x b) x c
    4. Bilangan 1 sebagai unsur identitas a x 1 = 1 x a = a
    5. Jika dikalikan dengan bilangan 0, maka hasilnya akan 0. a x 0 = 0 x a = 0
    6. Distributif untuk operasi penjumlahan dan pengurangan

    • a x (b + c) = (a x b) + (a x c)
    • a x (b-c) = (a x b) - (a x c)


    Sifat-Sifat Operasi Pembagian Bilangan Bulat

    Syarat utama pembagian a/b adalah b tidak boleh sama dengan 0. Jika b = 0, maka hasilnya tidak terdefinisi. Selain itu, sifat operasi pembagian bilangan bulat yang lainnya adalah tidak tertutup. Jika dan b adalah bilangan bulat, maka hasil a/b belum tentu bilangan bulat.


    Ayo Simak Video!

    https://www.youtube.com/watch?v=9eo-WaOcO4Y



    Diposting oleh di Tidak ada komentar:
    Langganan: Komentar (Atom)