Contoh Soal 1:
Suku ke-40 dari barisan 7, 5, 3, 1, … adalah …
Pembahasan:
Diketahui: a = 7
b = –2
ditanya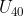
b = –2
ditanya
Jawab:
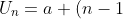b)
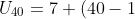(-2))
= 7 + 39 . (-2)
= 7 + (-78)
= – 71
Jadi, suku ke-40 barisan aritmatika tersebut adalah –71.
= 7 + 39 . (-2)
= 7 + (-78)
= – 71
Jadi, suku ke-40 barisan aritmatika tersebut adalah –71.
Contoh Soal 2:
Rumus suku ke-n dari barisan 5, –2, –9, –16, … adalah …
Pembahasan:
Diketahui: a = 5
b = –7
Ditanya: rumus suku ke-n barisan aritmatika tersebut = ?
Jawab:
Jadi, rumus suku ke-n barisan aritmatika tersebut adalah 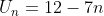
Contoh Soal 3:
Dalam suatu gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi pada baris ke-20 adalah …
Pembahasan:
Diketahui: a = 12
b = 2
Ditanyakan 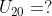
Jawab:
Jadi, banyaknya kursi pada baris ke-20 adalah 50 kursi.
Contoh Soal 4:
Rumus jumlah n suku pertama deret bilangan 2 + 4 + 6 + … + 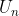 adalah …
adalah …
Pembahasan:
Diketahui: a = 2
b = 2
Ditanya: rumus jumlah n suku pertama barisan aritmatika tersebut = ?
Jawab:
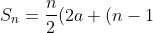b))
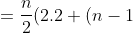2))
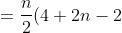)
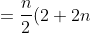)
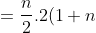)
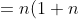)
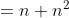
Jadi, rumus jumlah n suku pertama barisan aritmatika tersebut adalah 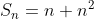
Contoh Soal 5:
Diketahui deret aritmatika dengan suku ke-3 adalah 24 dan suku ke-6 adalah 36. Jumlah 15 suku pertama deret tersebut adalah …
Pembahasan:
Diketahui 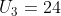
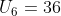
Ditanya: 
Jawab:
Sebelum kita mencari nilai dari  , kita akan mencari nilai a dan b terlebih dahulu dengan cara eliminasi dan subtitusi dari persamaan
, kita akan mencari nilai a dan b terlebih dahulu dengan cara eliminasi dan subtitusi dari persamaan  dan
dan  .
.
Sebelumnya mari ingat lagi bahwa 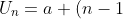b) sehingga
sehingga  dan
dan  dapat ditulis menjadi
dapat ditulis menjadi 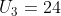
Eliminasi a menggunakan persamaan i dan ii.
a + 2b = 24
a + 5b = 36 –
-3b = -12

b = 4
a + 5b = 36 –
-3b = -12
b = 4
Lalu, substitusikan nilai b = 4 ke salah satu persamaan (contoh persamaan i).
a + 2b = 24
a + 2 . 4 = 24
a + 8 = 24
a= 24 – 8
a = 16
Setelah mendapatkan nilai a dan b, baru kita bisa mencari nilai dari 
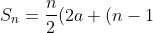b))
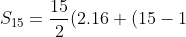4))
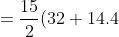)
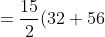)

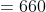
Jadi, jumlah 15 suku pertama deret tersebut adalah 660.
Tidak ada komentar:
Posting Komentar