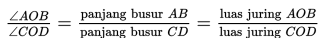Matematika
Kelas 9
Bangun Ruang Sisi Lengkung
3.7
Membuat generalisasi luas permukaan
dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)
4.7
Menyelesaikan masalah kontekstual
yang berkaitan dengan luas permukaan dan volume
bangun ruang sisi lengkung (tabung, kerucut, dan bola), serta gabungan beberapa
bangun ruang sisi lengkung
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait bangun ruang sisi lengkung, peserta didik dapat menghitung luas dan volume tabung.
Bangun Ruang Sisi Lengkung
Bangun ruang sisi lengkung adalah kelompok bangun ruang yang memiliki
bagian-bagian yang berbentuk lengkungan. Biasanya bangun ruang tersebut
memiliki selimut ataupun permukaan bidang. Yang termasuk ke dalam bangun ruang sisi
lengkung adalah tabung, kerucut, dan bola.
Tabung
Tabung merupakan sebuah bangun ruang yang dibatas oleh dua bidang berbentuk
lingkaran pada bagian atas dan bawahnya. Kedua lingkaran tersebut memiliki
ukuran yang sama besar serta kongruen. Keduanya saling berhadapan sejajar dan
dihubungkan oleh garis lurus. unsur-unsur yang ada pada tabung diantaranya
adalah:
t = tinggi tabung
r = jari-jari
π =
3,14 atau 
Rumus-Rumus Yang Berlaku untuk Tabung:
Luas Alas = Luas Lingkaran = πr2
Luas Tutup = Luas Alas = πr2
Luas Selimut = Keliling Alas × Tinggi = 2πr × t = 2πrt
Luas Permukaan Tabung = Luas Alas + Luas Tutup + Luas Selimut
Luas Permukaan Tabung = πr2 + πr2 + 2πrt
Luas Permukaan Tabung = 2πr2 + 2πrt
Luas Permukaan Tabung = 2πr(r + t )
Volume Tabung = Luas Alas × Tinggi
Volume Tabung = πr2 x t
Volume Tabung = πr2 t
Contoh Soal
1
Diketahui
sebuah tabung memiliki ukuran jari-jari 10 cm dan tinggi 30 cm. Maka coba
hitunglah:
- luas alas
tabung
- luas
selimut tabung
- luas
permukaan tabung
- volume tabung
Penyelesaiannya:
Luas alas
tabung
L = π r2
L = 3,14 x
10 x 10 = 314 cm2
Luas selimut
tabung
L = 2 π r t
L = 2 x 3,14
x 10 x 30
L = 1.884 cm2
Luas
permukaan tabung
Luas
permukaan tabung = luas selimut + luas alas + luas tutup (luas tutup = luas
alas)
L =
1884 + 314 + 314= 2512 cm2
Volume tabung
V = π r2 t
V = 3,14 x 10 x 10 x 30 = 9.432 cm3
Silahkan boleh amati juga video berikut agar lebih memahami materi diatas
https://www.youtube.com/watch?v=G0uDoggH0s8
Ayo Berlatih
1. Jari-jari alas sebuah tabung sama dengan tingginya. Jika jari-jari alasnya 10 cm, maka luas permukaan tabung adalah ....
2. Tentukan volume tabung yang jari-jari alasnya 7 cm dan tinggi 10 cm!
Kelas 8
Lingkaran
3.7 Menjelaskan
sudut pusat, sudut keliling, panjang busur, dan luas juring lingkaran, serta
hubungannya
4.7 Menyelesaikan
masalah yang berkaitan dengan sudut pusat, sudut keliling, panjang busur, dan
luas juring lingkaran, serta
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait lingkaran, peserta didik dapat menghitung luas dan keliling lingkaran.
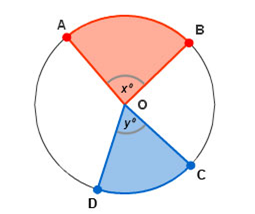
Mengingat kembali materi sebelumnya tentang Hubungan antara Sudut Pusat dengan Panjang Busur dan Luas Juring
perbandingan antara panjang busur AB dan CD memberikan hasil yang sama dengan perbandingan antara luas juring AOB dan COD.
Keliling dan luas lingkaran
Rumus luas lingkaran
L= π × r², dengan, π = konstanta pi (3.14 atau 22/7), dan r = jari-jari lingkaran.
Rumus keliling lingkaran
Sementara itu, rumus keliling lingkaran adalah 2 x π x r.
Contoh
1. Diketahui sebuah lingkaran memiliki diameter 28 cm. Berapakah luas dan keliling lingkaran tersebut?
Jawaban:
d = 28 cm
r = d/2 = 14 cm
Luas lingkaran
L = π x r2
= 22/7 x 14 x 14
= 22/7 x 142
= 616 cm2
Keliling Lingkaran
K = 2 x π x r
= 2 x 22/7 x 14
= 88 cm
Ayo berlatih
1. Diketahui lingkaran dengan jari-jari 20 cm, keliling lingkaran tersebut adalah …
2. Jika diketahui sebuah lingkaran mempunyai diameter 14 cm. Berapakah luas lingkaran tersebut?
3. Perhatikan gambar!
Tentukan keliling dan luas dari gambar tersebut!
Kelas 7
Capaian pembelajaran
Di
akhir fase D peserta didik dapat membuktikan teorema yang terkait dengan sudut
pada garis transversal, segitiga dan segiempat kongruen, serta segitiga dan
segiempat sebangun. Mereka dapat menggunakan teorema tersebut dalam menyelesaikan
masalah (termasuk menentukan jumlah besar sudut pada sebuah segitiga,
menentukan besar sudut yang belum diketahui pada sebuah segitiga, menghitung
tinggi dan jarak).
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait bangun datar, peserta didik dapat memahami
arti garis, segmen garis, dan sinar garis, serta cara menyatakan sudut, arti
tegak lurus dan sejajar serta cara menyatakannya, dan dapat memahami jarak antara dua titik,
jarak antara titik dan garis, dan jarak di antara dua garis sejajar.
Garis adalah susunan titik–titik yang saling bersebelahan serta berderet memanjang ke dua arah (kanan kiri atau atas bawah).
Sudut adalah ruang yang terbentuk di antara dua garis yang saling berpotongan. Sudut juga bisa diartikan sebagai daerah yang dibatasi oleh dua garis, serta dapat digambarkan sebagai pertemuan antara dua garis. Dalam sebuah sudut terdapat beberapa bagian membentuknya, meliputi: Kaki sudut merupakan sinar garis yang membentuk sudut tersebut. Titik sudut merupakan titik pangkal atau titik potong sinar garis. Daerah sudut merupakan daerah yang berada di antara dua kaki sudut (interior angle).
jenis jenis sudut menurut besar sudutnya yaitu meliputi:
- Sudut lancip ialah sudut yang memiliki besar kurang dari 90° (0° – 90°).
- Sudut siku siku ialah sudut yang memiliki besar 90°.
- Sudut tumpul ialah sudut yang memiliki besar lebih dari 90° (90° – 180°).
- Sudut lurus ialah sudut yang memiliki besar 180°.
- Sudut refleks ialah sudut yang mempunyai besar lebih dari 180° (180° – 360°).