Math

 Matematika

Kelas 8

Lingkaran

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Agenda hari ini adalah menyelesaiakan soal-soal yang berkaitan dengan lingkaran sebagai penilaian harian.

Paket 1

1. Hitunglah luas gambar dibawah ini!

     2.    Luas tembereng yang diarsir pada gambar berikut adalah...

3. 

Jika sudut ABC = 60° dan titik O adalah pusat lingkaran maka sudut  AOC = …

1.    4. Jika diketahui OA=4 cm, dan PB=2 cm dan OP=10 cm. Panjang garis singgung persekutuan dalam dua lingkaran tersebut adalah...

Paket 2

1. Hitunglah luas gambar dibawah ini!

2. Panjang busur lingkaran dengan sudut pusat 72° dan panjang jari-jari 10 cm adalah...

3. Tentukan besar ∠ ACB

4. Diketahui dua lingkaran dengan pusat P dan Q, jarak PQ= 26 cm, panjang jari-jari lingkaran masing-masing 12 cm dan 2 cm. Hitung panjang garis singgung persekutuan luar kedua lingkaran!

Math

 Matematika

Kelas 9

Kesebangunan dan Kekongruenan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Agenda hari ini adalah menyelesaiakan soal-soal yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar sebagai penilaian harian.

Paket 1

1. Perhatikan gambar berikut.
Segitiga $���$ kongruen dengan segitiga $���$. Pasangan sudut yang sama besar adalah ... $\cdots \cdot$

2. Diberikan dua buah persegipanjang ABCD dan persegipanjang PQRS seperti gambar berikut.

Kedua persegipanjang tersebut adalah sebangun. Tentukan panjang PQ ....

3. Perhatikan gambar!

Jika $DE:DA=2:5$, maka panjang $EF$ adalah...

Paket 2

1. Dua segitiga pada gambar di bawah adalah kongruen

Pasangan sisi yang sama panjang adalah 

2. Perhatikan gambar berikut!

Tentukan panjang DE

3. Dari soal berikut ini tentukan panjang EF!

Kelas 7

Aritmetika Sosial

3.9          Mengenal dan menganalisis berbagai situasi terkait aritmetika sosial (penjualan, pembelian, potongan, keuntungan, kerugian, bunga tunggal, persentase,  bruto, neto, tara)

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait aritmetika sosial, peserta didik dapat:

mengenal fenomena atau aktivitas yang terkait dengan aritmetika sosial (penjualan, pembelian, potongan, keuntungan, kerugian, bunga tunggal, persentase, bruto, neto, tara)

Mendapatkan informasi yang terkait dengan artimetika sosial

Menentukan hubungan antara penjualan, pembelian, untung, dan rugi

Memahami Keuntungan dan Kerugian

Ayo Kita Amati!

Pak Subur Tukang Bubur Ayam

PakSubur seorang penjual bubur ayam di daerah Jakarta. Seperti biasa,setiap pagi Pak Subur pergi ke pasar untuk berbelanja bahan pokok untuk membuat bubur ayam. Untuk membeli bahan pokok bubur tersebut, Pak Subur menghabiskan uang Rp1.000.000,00. Dengan bahan baku tersebut Pak Subur mampu membuat sekitar 130 porsi bubur ayam dan dijual dengan harga Rp10.000,00 per porsi. Pada hari itu Pak Subur mampu menjual 110 porsi bubur ayam.

Pak Soso Tukang Bakso

Pak Soso seorang penjual bakso di daerah Malang. Setiap hari Pak Soso menghabiskan Rp800.000,00 untuk berbelanja bahan baku untuk membuat bakso. Dengan bahan baku tersebut Pak Soso mampu membuat rata-rata 120 porsi dengan harga Rp8.000,00 per porsi. Pada hari itu terjadi hujan di tempat Pak Soso biasa berjualan, sehingga bakso yang laku terjual hanya 90 porsi.

Pak Sarto Tukang Sate

Pak Sarto seorang penjual sate di daerah Madura. Setiap hari Pak Sarto menghabiskanRp700.000,00 rupiah untuk berbelanja bahan baku untuk membuat sate. Dengan bahan baku tersebut Pak Sarto mampu membuat rata-rata 100 porsi dengan harga Rp10.000,00 per porsi. Pada hari itu terjadi hujan di tempat Pak Sarto biasa berjualan, sehingga sate yang laku terjual hanya 70 porsi.

 

1.    Persentase keuntungan

Untuk menghitung Persentase Keuntungan kita dapat menggunakan rumus

PU = HJ – HB /HB  x 100%

PU = Persentase keuntungan

HB = harga beli (modal)

HJ = harga jual (total pemasukan)

Atau dapat juga menggunakan rumus

U = HJ – HB

U% = U/HB x 100%

Contoh Soal

1.    Pak Dedi membeli suatu motor bekas dengan harga Rp4.000.000,00. Dalam waktu satu minggu motor tersebut dijual kembali dengan harga Rp4.200.000,00. Tentukan persentase keuntungan Pak Dedi

Pembahasan :

Diketahui :

HB = 4.000.000

HJ = 4.200.000

Ditanyakan U%

U = HJ – HB

4.200.000 – 4.000.000 = 200.000

U% = U/HB x 100%

200.000/4.000.000 x 100%

= 2/4 x 10%

= 20/4

= 5%

2.    Pak Dedi membeli suatu motor bekas dengan harga Rp4.000.000,00. Dalam waktu satu minggu motor tersebut dijual kembali dengan harga 105% dari harga beli. Tentukan keuntungan Pak Dedi.

Pembahasan :

Diketahui :

HB = 4.000.000

HJ% = 105%

Ditanyakan U ?

U = HJ – HB

HJ = HJ% x HB

= 105% x 4.000.000

= 105/100 x 4.000.000

= 105 x 40.000

= 4.200.000

U = HJ – HB

= 4.200.000 – 4.000.000

= 200.000 

Keuntungannya = Rp200.000

 

2.    Persentase Kerugian

Untuk menghitung persentase kerugian dapat ditentukan dengan rumus :

PR = HB – HJ/HB x 100%

Atau : 

R = HB – HJ

R% = R/HB x 100%

Contoh Soal

1.    Pak Rudi membeli sepetak tanah dengan hargaRp40.000.000,00.Karena terkendala masalah keluarga, Pak Dedi terpaksa menjual tanah tersebut dengan harga Rp38.000.000,00. Tentukan persentase kerugian yang ditanggung oleh Pak Rudi.

Pembahasan :

Diketahui :

HB = 40.000.000

HJ = 38.000.000

Ditanyakan R%?

R = HB – HJ

= 40.000.000 – 38.000.000

= 2.000.000

Persentase kerugian =

R% = R/HB x 100%

= 2.000.000/40.000.000 x 100%

= 2/4 x 10%

= 20/4%

= 5%

 

Ayo berlatih pada pada pertemuan hari ini dari buku cetak halaman 75-76.

Akan kita selesaiakn soal no 1, 7 dan 9.

Math

 Matematika

Kelas 9

Kesebangunan dan Kekongruenan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Agenda hari ini adalah membahas soal-soal persiapan penilaian harian pada pertemuan berikutnya.

1. Pada gambar berikut, segitiga PQR dan segitiga STU merupakan dua segitiga kongruen. Besar ∠R=∠U dan ∠Q=∠S . Manakah pasangan sisi yang sama panjang?

Dari informasi sudut pada segitiga di atas dapat kita peroleh sisi yang sama panjang yaitu sisi di depan sudut yang sama besar, PR=TU

2. Sebuah pohon yang berada di depan gedung mempunyai tinggi 8 m. Pada saat yang sama bayangan gedung berimpit dengan bayangan pohon seperti tampak pada gambar di bawah.

Tinggi gedung sesuai ukuran adalah?

seperti berikut ini;

Dari gambar di atas kita peroleh bahwa $△ABC$ sebangun dengan $△ADE$, sehingga berlaku:
$\begin{array}{cc}\frac{AB}{AD}& =\frac{BC}{DE}\\ \frac{10}{15}& =\frac{8}{DE}\\ DE& =\frac{8\times 15}{10}\\ DE& =12\end{array}$

3. Pada gambar berikut, segitiga KLM

$��\mathrm{�<span\; style="font-family:\; "Noto\; Sans",\; sans-serif;\; font-size:\; 15.52px;"> </span><span\; style="font-family:\; "Noto\; Sans",\; sans-serif;\; font-size:\; 15.52px;">kongruen\; dengan\; segitiga</span><span\; style="font-family:\; "Noto\; Sans",\; sans-serif;\; font-size:\; 15.52px;"> <span\; style="font-family:\; MJXc-TeX-math-I,\; MJXc-TeX-math-Ix,\; MJXc-TeX-math-Iw;\; font-size:\; 18.7792px;\; white-space:\; pre;">R</span><span\; style="font-family:\; MJXc-TeX-math-I,\; MJXc-TeX-math-Ix,\; MJXc-TeX-math-Iw;\; font-size:\; 18.7792px;\; white-space:\; pre;">S</span><span\; style="font-family:\; MJXc-TeX-math-I,\; MJXc-TeX-math-Ix,\; MJXc-TeX-math-Iw;\; font-size:\; 18.7792px;\; white-space:\; pre;">T</span></span>}$$��\mathrm{<br>}$Pernyataan yang sama panjang adalah...

Segitiga $KLM$ dan $RST$ kongruen, maka:

• $\angle K=\angle R={75}^{\circ }$
• $\angle L=\angle S={35}^{\circ }$
• $\angle M=\angle T={70}^{\circ }$
• $KM=RT$
• $ML=TS$
• $KL=RS$

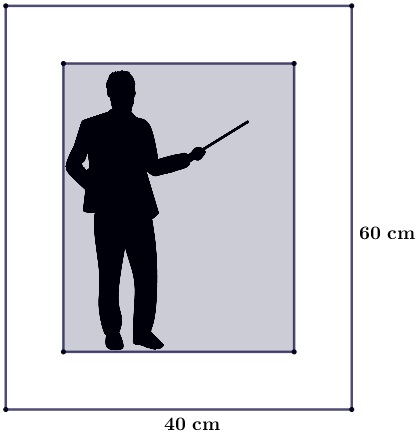
4. Sebuah foto ditempelkan pada selembar karton. Di sebelah atas, kiri, dan kanan foto masih tersisa karton selebar 3 cm.

$3\text{cm}$Jika foto dan karton sebangun, luas karton yang tidak tertutup adalah...

Disampaikan pada soal di sebelah atas, kiri, dan kanan foto masih tersisa karton selebar $3\text{cm}$, sedangkan pada bagian bawah belum diketahui. Sehingga apabila kita gambarkan ukurannya dapat seperti berikut ini.

Foto dan karton sebangun, sehinga berlaku:
$\begin{array}{cc}\frac{40}{34}& =\frac{60}{57-x}\\ \frac{2}{34}& =\frac{3}{57-x}\\ \left(2\right)(57-x)& =\left(3\right)\left(34\right)\\ 114-2x& =102\\ -2x& =102-114\\ -2x& =-12⟶x=6\end{array}$

Luas karton tidak tertutup foto adalah:
$\begin{array}{cc}L& =L_{\text{karton}}-L_{\text{foto}}\\ & =40\times 60-34\times 51\\ & =2.400-1.734\\ & =666\end{array}$

Kelas 8

Lingkaran

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Agenda hari ini adalah membahas soal-soal persiapan penilaian harian pada pertemuan berikutnya.

1. Panjang busur lingkaran dengan sudut pusat adalah...

Untuk menghitung panjang busur lingkaran kita membutuhkan keliling lingkaran $\left(k=2\pi r\right)$. Dengan menggunkan $\pi =3,14$, kita akan peroleh:
$\begin{array}{cc}\text{panjang busur}& =\text{keliling lingkaran}\times \frac{\text{sudut pusat}}{{360}^{\circ }}\\ & =2\pi r\times \frac{{72}^{\circ }}{{360}^{\circ }}\\ & =2\cdot 3,14\cdot 10\times \frac{1}{5}\\ & =12,56\end{array}$

2. Perhatikan gambar!

$AC$ merupakan diameter lingkaran yang berpusat di titik $O$. Jika besar $\angle BOA={100}^{\circ }$, maka $\angle CDB=\cdots$

Dari gambar $\angle BOA={100}^{\circ }$ maka $\angle BOC={80}^{\circ }$ karena $\angle BOA$ dan $\angle BOC$ adalah sudut pelurus.

$\angle BOC$ adalah sudut pusat lingkaran dan $\angle CDB$ adalah sudut keliling lingkaran maka berlaku $\angle BOC=2\angle CDB$.
$\begin{array}{cc}2\angle CDB& =\angle BOC\\ 2\angle CDB& ={80}^{\circ }\\ \angle CDB& =\frac{{80}^{\circ }}{2}\\ \angle CDB& ={40}^{\circ }\end{array}$

3. Panjang tali yang dibutuhkan untuk mengikat 3 batang kayu bila diameter kayu 

$14$ dm adalah...$3$

Sebagai ilustrasi menghitung panjang tali yang dibutuhkan (*minimum) untuk mengikat ketiga kayu diatas, kurang lebih seperti berikut ini:

Dari gambar diatas kita peroleh panjang tali minimum yang dibutuhkan adalah $3\times (DE+EF)$, dimana $DE=14$ dan $EF$ adalah busur lingkaran.

Dari gambar juga dapat kita peroleh besar sudut: $\measuredangle ABC={60}^{\circ }$; $\measuredangle ABE={90}^{\circ }$; $\measuredangle CBF={90}^{\circ }$ sehingga besar $\measuredangle EBF={120}^{\circ }$.

Panjang busur $EF$;
$\begin{array}{cc}EF& =\frac{120}{360}\times 2\pi r\\ & =\frac{1}{3}\times 2\frac{22}{7}\cdot 7\\ & =\frac{44}{3}\end{array}$

Panjang tali minimum adalah $3\times (DE+EF)=3\times (14+\frac{44}{3})$
$\begin{array}{cc}3\times (DE+EF)& =3\times \left(14+\frac{44}{3}\right)\\ & =42+44\\ & =86dm\\ & =8.600cm\end{array}$

4. P adalah pusat lingkaran yang kelilingnya 4πcm ∠APB=50∘

$\mathrm{\angle }���={50}^{\circ }$ Luas daerah di arsir adalah...$4��\mathrm{�<span\; style="font-family:\; "Noto\; Sans",\; sans-serif;\; font-size:\; 15.52px;">,\; dan </span>}$$�$ 

Keliling lingkaran $4\pi cm$ maka $2\pi r=4\pi$ dan $r=2$.
Luas daerah yang diarsir adalah
$\frac{130}{360}\times \pi r^2$
$=\frac{13}{36}\times \pi 2^2$
$=\frac{13}{36}\times \pi 4$
$=\frac{13}{9}\times \pi$

Kelas 7

Perbandingan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Agenda hari ini adalah membahas soal-soal penilaian harian.

1.      1. Diketahui tinggi badan Nayla adalah 160 cm dan tinggi badan Reyka 140 cm. Tentukanlah perbandingan tinggi badan Nayla dengan Reyka!

2.   2.    Harga 1 lusin pensil adalah Rp 60.000 lalu berapa harga yang harus dibayarkan jika Dzaki hanya membeli 6 buah pensil saja? 

3.    3.   Sebuah motor berhasil menempuh jarak 152 km dan membutuhkan bahan bakar sebanyak 20 liter. Lalu berapa banyak bahan bakar yang digunakan jika pengendara mengendarai kendaraan dan menempuh jarak 500 km?

4.   4.    Seorang peternak memiliki pakan untuk sapi sebanyak 30 ekor. Pakan tersebut hanya cukup digunakan untuk 20 hari saja. Lalu apabila peternak membeli 5 ekor sapi lagi berapa lama pakan tersebut akan habis?

Pembahasan:

1. Nayla:Rayka =160:140 = 16:14 = 8: 7

2. 1 lusin pensil = Rp 60.000 

     6 buah pensil = setengah lusin  maka Rp 60.000:2 = Rp 30.000

     atau

     Rp 60.000:12 = Rp 5.000

    maka 6 pensil x Rp 5.000 = Rp 30.000

3. 152/500 = 20/x

    x = (500 x 20)/152 = 65,8 liter

4. 30/35 = x/20

x = (30x20)/35 = 17 hari