Math

 Matematika

Kelas 9

Kesebangunan dan Kekongruenan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait perbandingan, peserta didik dapat menentukan kesebangunan dan kekongruenan segitiga-segitiga sebangun dan menentukan kesebangunan dan kekongruenan segitiga-segitiga kongruen.

Kesebangunan

Rumus Kesebangunan pada Segitiga Siku-Siku

Dua buah segitiga yang sebangun, di mana kedua segitiga memiliki besar sudut – sudut yang bersesuaian sama besar. Didapatkan persamaan yang menyatakan perbandingan sisi – sisi yang bersesuaian dari kedua segitiga.

segitiga.

AB/PQ = BC/QR = AC/PR

Sudut A = Sudut P

Sudut B = Sudut Q

Sudut C = Sudut R

 

Contoh

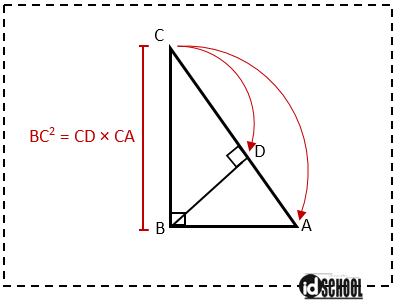
Perhatikan gambar!

Pada gambar tersebut, panjang KM adalah ….

Pembahasan:
Menghitung panjang KM:
KM2 = KN × KL
KM2 = 15 × (15 + 10)
KM2 = 15 × 25 = 375
KM = √375
Jadi, panjang KM adalah √375.

Kekongruenan

Kongruen adalah benda-benda yang memiliki bentuk dan ukuran yang sama. Dua buah bangun atau lebih dapat dikatakan saling kongruen jika memenuhi dua syarat: 

1. Pasangan sisi-sisi yang bersesuaian sama panjang 

2. Besar sudut yang bersesuaian sama besar.

Perbedaan antara Kesebangunan dan Kekongruenan pada Segitiga

Gambar

                  (s, s, s)                                            (s, sd, s)                                       (sd, s, sd)

                

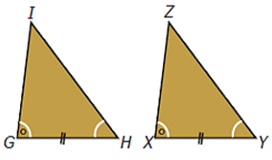
Contoh 1

Perhatikan gambar berikut.

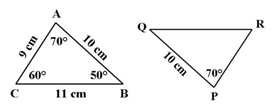
Jika ΔABC kongruen dengan ΔPQR, maka tentukan:
- panjang PR
- panjang QR
- ∠PQR
- ∠QRP

Penyelesaian:

• Oleh karena sisi PR bersesuaian dengan AC, maka panjang sisi PR = AC = 9 cm.
• Oleh karena sisi QR bersesuaian dengan CB, maka panjang QR = CB = 11 cm.
• Oleh karena ∠PQR bersesuaian dengan ∠ABC, maka ∠PQR = ∠ABC = 50⁰.
• Oleh karena ∠QRP bersesuaian dengan ∠ACB, maka ∠ QRP = ∠ ACB = 60⁰.

Contoh 2

Perhatikan gambar segitiga siku-siku di bawah ini.

Tentukan nilai x yang memenuhi agar segitiga siku-siku ABC kongruen dengan segitiga siku-siku PQR.

Penyelesaian:

Dua segitiga dikatakan kongruen jika semua sisi yang besesuaian sama panjang. Oleh karena itu, sisi AB = PQ, AC = PR dan BC = QR.

Panjang sisi BC dapat ditentukan dengan menggunakan teorema Pythagoras, yaitu:

BC2=AB2+AC2

⇔BC=AB2+AC2−−−−−−−−−−√

⇔BC=62+82−−−−−−√

⇔BC=36+64−−−−−−√

⇔BC=100−−−√

⇔BC=10

⇔BC=QR

⇔10=3+x

⇔x=10−3=7

Jadi, nilai x yang memenuhi agar segitiga siku-siku ABC kongruen dengan segitiga siku-siku PQR adalah 7 cm.