Matematika
Kelas IX
Transformasi Geometri
Pertemuan 1
Elemen Geometri
Media/alat peraga: Laptob dan LCD
Capaian Pembelajaran
Peserta didik dapat melakukan transformasi tunggal (refleksi, translasi, rotasi, dan dilatasi) titik, garis, dan bangun datar pada bidang koordinat Kartesius dan menggunakannya untuk menyelesaikan masalah.
Tujuan Pembelajaran
Peserta didik dapat melakukan transformasi tunggal refleksi
Assalamualaikum Wr. Wb.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
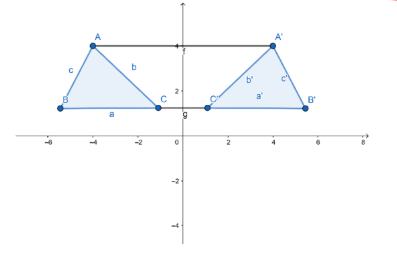
- Berikut adalah rumus-rumus pencerminan suatu objek
- Sumbu x = (x,y)-> (x,-y)
- Sumbu y = (x, y)-> (-x, y)
- Titik asal (0,0) -> (x,y) = (-x, -y)
- Garis x =y -> (x’,y’) = (-y ,-x)
- Garis x = -y -> (x’,y’) = (-y, -x)
- Garis y =h -> (x’,y’) = (x/ 2h-y)
- Garis x = k -> (x’y’) = (2k -x/y)
Ayo simak video berikut:
Matematika
Kelas VIII
Relasi dan Fungsi
Pertemuan 3
Media/alat peraga: Laptob dan LCD
Elemen
Aljabar
Capaian Pembelajaran
Memahami relasi dan fungsi (domain, kodomain, range) dan menyajikannya dalam bentuk diagram panah, tabel, himpunan pasangan berurutan, dan grafik. Mereka dapat membedakan beberapa fungsi nonlinear dari fungsi linear secara grafik
Tujuan Pembelajaran
Peserta didik dapat memahami relasi dan fungsi (domain, kodomain, range) dan menyajikannya dalam bentuk diagram panah, tabel, himpunan pasangan berurutan, dan grafik.
- Peserta didik dapat menentukan nilai korespondensi satu-satu
Assalamualaikum Wr. Wb.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tidak ada komentar:
Posting Komentar