Matematika Kelas IX
Transformasi Geometri
Pertemuan 13
Elemen Geometri
Media/alat peraga: Laptob dan LCD
Capaian Pembelajaran
Tujuan Pembelajaran
Peserta didik dapat melakukan transformasi tunggal dilatasi
Assalamualaikum Wr. Wb.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Rotasi
Secara umum, rotasi suatu titik dibagi menjadi dua, yakni rotasi terhadap titik pusat (0,0) dan rotasi terhadap titik (a,b).
Titik Asal | Rotasi | Titik Bayangan |
(x,y) | (0,90°) | (-y,x) |
(x,y) | (0,-90°) | (y,-x) |
(x,y) | (0,180°) | (-x,-y) |
(x,y) | (0,-180°) | (-x,-y) |
(x,y) | (0,270°) | (y,-x) |
(x,y) | (0,-270°) | (-y,x) |
Dilatasi
Rumus dilatasi tititk P (x, y) dengan titik pusat O(0, 0) dan faktor skala K.
P(x, y) = P'(Kx, Ky)
Rumus dilatasi tititk P (x, y) dengan titik pusat (a, b) dan faktor skala K.
Matematika Kelas VIII
Fungsi Linear
Pertemuan 8
Elemen Aljabar
Media/alat peraga: Laptob dan LCD
Capaian Pembelajaran
Peserta didik dapat menyajikan, menganalisis, dan menyelesaikan masalah dengan menggunakan persamaan linear;
Assalamualaikum Wr. Wb.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Fungsi linear ini tidak akan jauh dari yang namanya penggambaran grafik, sehingga ketika harus melakukannya harus mencermati beberapa langkah berikut ini.
- Menentukan titik potong dengan sumbu x, maka y = 0, didapatkan dari koordinat A (x1, 0)
- Menentukan titik potong dengan sumbu y, maka x = 0, didapatkan dari koordinat B (0, y1)
- Menghubungkan dua titik A dan B, sehingga akan membentuk garis lurus persamaan linear yang kemudian ditulis dengan y = ax + b.
- Apabila b bernilai positif, maka fungsi linear akan dilukis garis dari arah kiri bawah ke kanan atas.
- Apabila b bernilai negatif, maka fungsi linear akan dilukis garis dari arah kiri atas ke kanan bawah.
- Apabila b bernilai 0, maka fungsi linear akan dilukis garis yang sejajar dengan sumbu datar X.
Secara umum, bentuk persamaan garis lurus ada dua macam, sehingga cara untuk menentukan gradiennya juga berbeda beda, tergantung dari bentuk persamaan garisnya.
a. Persamaan garis y = mx + c
Pada persamaan garis ini, gradiennya adalah koefisien dari variabel x itu sendiri, yaitu m.
Contoh: Garis y = 3x + 2, koefisien x adalah 3. Jadi, gradien garis tersebut adalah 3.
b. Persamaan garis ax + by + c = 0
Jika diketahui persamaan garis ax + by + c = 0, maka langkah pertama yang harus kamu lakukan adalah ubah persamaan garis tersebut ke bentuk y = mx + c, dengan m adalah gradien garis tersebut.
Contoh: Hitunglah kemiringan (gradien) pada persamaan garis 5x + 2y – 8 = 0
Penyelesaian:
Cara 1: Ubah dulu persamaan 5x + 2y – 8 = 0 ke bentuk y = mx + c, sehingga persamaannya menjadi,
5x + 2y – 8 = 0
2y = -5x + 8
y = (-5/2)x + 4
Jadi, gradien dari persamaan garis tersebut adalah -5/2.Cara Mencari Persamaan Garis
1. Persamaan garis lurus melalui titik (x1,y1) dan bergradien m
Jika sebuah garis yang bergradien m melalui titik (x1,y1), rumus persamaan garis lurusnya adalah sebagai berikut

contoh
Tentukan persamaan garis lurus yang melalui titik (6,-2) dan bergradien 2.
Pembahasan
Adapun nilai x1 = 6 dan y1 = -2, m = 2.
Dengan demikian, persamaan garis lurusnya adalah sebagai berikut.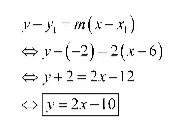
Jadi, persamaan garisnya adalah y = 2x – 10.
2. Persamaan garis lurus melalui 2 titik, yaitu A(x1,y1) dan B(x2,y2)
Jika sebuah garis lurus melalui 2 titik A(x1,y1) dan B(x2,y2), maka persamaan garisnya ditentukan dengan rumus berikut..

contoh
Tentukan persamaan garis yang melalui titik P(4,-2) dan Q(-1,3)!
Pembahasan
Untuk mencari persamaan garisnya, gunakan persamaan berikut.

Jadi, persamaan garis lurus yang melalui titik P(4,-2) dan Q(-1,3) adalah x + y – 2 = 0.


.png)


Tidak ada komentar:
Posting Komentar