Math

Matematika

Kelas IX

Bilangan Berpangkat dan Bentuk Akar

Pertemuan 6

Media/alat peraga: Laptob dan LCD

Capaian Pembelajaran

Peserta didik dapat membaca, menulis, dan membandingkan bilangan  bulat, bilangan rasional dan irasional, bilangan desimal. Bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.

Tujuan Pembelajaran

Peserta didik dapat menentukan bilangan berpangkat bulat dan akar, bilangan dalam  notasi ilmiah.. 

- menyederhanakan bentuk akar

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

Ayo simak materi!

Mari kita ingat kembali materi pada pertemuan sebelumnya tetang bilangan berpangkat pecahan dan bentuk akar.

Bentuk akar adalah akar dari bilangan rasional yang hasilnya merupakan bilangan irasional.
Bilangan Irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk $\frac{a}{b}$ dimana $a,b$ bilangan bulat dan $b\ne 0$.

Misalnya $\sqrt{5}$, $\sqrt{7}$, $\sqrt{11}$, dan bentuk lainnya. Sedangkan $\sqrt{4}=2$ atau $\sqrt{\frac{9}{4}}=\frac{3}{2}$ bukan bentuk akar karena hasilnya adalah bilangan rasional.

Secara umum bentuk akar ini dituliskan dalam bentuk $\sqrt[n]{na}=a^{\frac{1}{n}}$.
dibaca: "akar pangkat $n$ dari $a$".

Bentuk khusus $\sqrt[n]{na}$, yaitu saat $n=2$ dapat tidak dituliskan, sehingga dapat ditulis hanya dengan $\sqrt{a}$ dibaca "akar kuadrat dari $a$" atau "akar pangkat dua dari $a$" atau sering disebut hanya dengan "akar $a$".

Ayo simak video berikut:

https://www.youtube.com/watch?v=CLybFz7eFB8&list=PL25RrvlGWE3BLvfWRvkZ2ch9IpGjPSO3H&index=5

Ayo Berlatih!

1. Bentuk sederhana dari √300 adalah ...
2. Hitunglah hasil dari √5 x √20
3. Hitunglah hasil dari 
4. Hitunglah hasil dari 2√3 + 5√3 = ....

Matematika

Kelas VIII

Pola Bilangan

Pertemuan 6

Media/alat peraga: Laptob dan LCD

Capaian Pembelajaran

Memprediksi dan menggeneralisasi pola dalam bentuk susunan benda dan bilangan.

Tujuan Pembelajaran

Peserta didik dapat mengenali, memprediksi dan menggeneralisasi pola dalam  bentuk susunan benda(obyek) dan pola bilangan

- Memprediksi pola deret geometri

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.

Ayo simak materi!

Barisan geometri adalah pola yang memiliki pengali atau rasio yang tetap untuk setiap 2 suku yang berdekatan. Rasio pada barisan geometri biasa disimbolkan dengan r. Barisan geometri juga biasa disebut sebagai barisan ukur.

Contoh lebih mudahnya begini, misal kamu punya barisan seperti ini:

1, 3, 9, 27, …

 

Dari barisan tersebut, kita bisa lihat antara suku pertama dengan suku kedua, antara suku kedua dan suku ketiga dan seterusnya selalu punya pengali yang tetap, yaitu 3. Dengan demikian, barisan ini termasuk barisan geometri.

Rumus Jumlah Suku ke-n (Sn) pada Barisan dan Deret Geometri

Sn adalah jumlah suku ke-n pada barisan dan deret. Nah, bagaimana cara kita mencari tau Sn pada barisan geometri dan deret geometri? Berikut ini adalah rumusnya.

Contoh:

Diketahui barisan geometri:

1, 3, 9, 27, 81, ….

Hitunglah jumlah 3 suku pertamanya

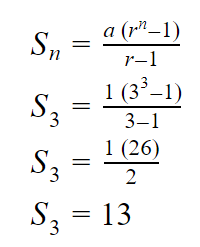
Jadi, S3 dari barisan geometri tersebut adalah 13.

Ayo Simak Video!

https://www.youtube.com/watch?v=-t1MlqJ_Z2A&t=5s

Ayo Berlatih!

1. Tentukan jumlah 10 suku pertama dari deret 3+6+12+ ...

2. Suatu deret 5+15+45+ ... Berapakah jumlah 6 suku pertamanya?