Matematika Kelas VII
Perbandingan
Pertemuan 3
Elemen Geometri
Media/alat peraga: Laptob dan LCD
Capaian Pembelajaran
Murid dapat menggunakan rasio (skala, proporsi, dan laju perubahan) dalam penyelesaian masalah.
Tujuan Pembelajaran
Peserta didik dapat menggunakan rasio (skala, proporsi, dan laju perubahan) dalam penyelesaian masalah.
- peserta didik dapat menggunakan rasio
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Ayo simak materi!
Perbandingan berbalik nilai merupakan kebalikan dari perbandingan senilai. Jika nilai awal pada perbandingan ini besar, nilai akhirnya menjadi semakin kecil. Namun, jika nilai awal semakin kecil, maka nilai akhirnya semakin besar.
Rumus perbandingan berbalik nilai
Hubungan perbandingan berbalik nilai dapat dinyatakan dalam bentuk persamaan berikut:
Agar lebih paham mari simak video berikut!
https://www.youtube.com/watch?v=sop63Y5SSV4
Ayo Berlatih!
1. Sebuah pekerjaan dapat selesai 20 hari dengan 10 orang. Jika jumlah pekerja ditambah menjadi 25 orang, berapa lama pekerjaan selesai?
2. Seorang pemborong mampu menyelesaikan pekerjaan 6 bulan dengan 21 orang. Jika harus selesai dalam 4,5 bulan, berapa pekerja yang diperlukan?
Kekongruenan dan Kesebangunan
Pertemuan 4
Elemen Geometri
Media/alat peraga: Laptob dan LCD
Capaian Pembelajaran
menjelaskan sifat-sifat kekongruenan dan kesebangunan pada segitiga dan segiempat, dan menggunakannya untuk menyelesaikan masalah
Tujuan Pembelajaran
Peserta didik dapat menjelaskan sifat-sifat kekongruenan dan kesebangunan pada segitiga dan segiempat, dan menggunakannya untuk menyelesaikan masalah
- peserta didik dapat menentukan panjang sisi yang belum diketahui
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Ayo simak materi!
Kesebangunan adalah istilah yang digunakan untuk menyatakan dua bangun datar yang memiliki proporsi yang mirip satu sama lain.
Syarat Kesebangunan pada Bangun Datar
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian memiliki perbandingan yang sama
Contoh
Hitunglah panjang sisi yang belum diketahui dari bentuk kesebangunan berikut.
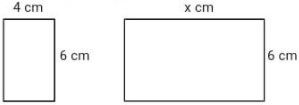
Jawaban:
4 . x = 6 . 6
4x = 36
x = 36/4
x = 9
Ayo Simak video berikut!
Ayo berlatih!
1. Perhatikan gambar berikut!
Nilai x adalah ....
2. Perhatikan gambar berikut!
Panjang LM = 30 cm dan LK = 24 cm, maka panjang KN adalah ....