Matematika
Kelas 9
Kekongruenan dan kesebangunan
3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait kesebangunan, peserta didik dapat mengidentifikasi syarat-syarat kesebangunan
dengan baik dan benar
Pengertian
Kesebangunan bangun datar digunakan untuk membandingkan dua buah bangun datar (atau lebih) dengan bentuk yang sama. Dua buah bangun datar dapat dikatakan sebangun apabila panjang setiap sisi pada kedua bangun datar tersebut memiliki nilai perbandingan yang sama.
Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan.
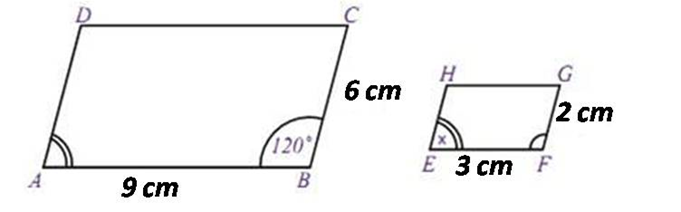
Berikut ini adalah dua buah bangun datar ABCD dan
EFGH
Apakah kedua
bangun datar ABCD dan EFGH sebangun? Untuk dapat menjawabnya, lakukanlah
langkah langkah berikut.
Pembahasan
a.
Periksalah bentuk bangun di atas.
Bentuk Bangun ABCD adalah ...
Bentuk Bangun EFGH adalah ...
Berdasarkan bentuk bangun di atas,
maka sifat sifat bangun datar ................................... yang
berkaitan dengan sudut dan sisi adalah..
1. Sisi sisi yang berhadapan dan sejajar memiliki ..... yang sama
2. Sudut sudut yang berhadapan memiliki ....... yang sama.
b.
Periksalah sudut sudut pada kedua bangun.
Pada Bangun ABCD :
ÐA = ...
ÐB = ...
ÐC = ...
ÐD = ...
Pada Bangun EFGH :
ÐE = ...
ÐF = ...
ÐG = ...
ÐH = ...
Lalu,
perhatikanlah bangun diatas,
Maka
Sudut – sudut yang bersesuaian antara
bangun ABCD dan EFGH adalah
ÐB dengan ÐF besarnya 1200
ÐA dengan ÐE besarnya .....0
Ð... dengan
Ð... besarnya
.....0
Ð... dengan
Ð... besarnya
.....0
c.
Periksalah Sisi – sisi pada kedua bangun:
Pada Bangun
ABCD :
Sisi AB = ...
Sisi BC = ...
Sisi CD = ...
Sisi DA = ...
Pada Bangun EFGH :
Sisi EF = ...
Sisi FG = ...
Sisi GH = ...
Sisi HE = ...
Lalu,
perhatikanlah kembali bangun diatas,
Maka
sisi sisi yang bersesuaian antara bangun
ABCD dan EFGH adalah
AB dengan
EF panjangnya 9 cm
dan 3 cm
.... dengan .... panjangnya .... cm dan .... cm
BC dengan
FG panjangnya
.... cm dan .... cm
.... dengan .... panjangnya .... cm dan .... cm
Maka Perbandingan sisi yang bersesuaian
:
Dari masalah di atas dapat kita simpulkan
bahwa
kedua bangun ......
ABCD dan
....
EFGH adalah ...
Kelas 8
Lingkaran
3.7 Menjelaskan sudut pusat, sudut keliling, panjang busur, dan luas juring lingkaran, serta hubungannya
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini adalah peserta didik dapat memahami konsep garis singgung lingkaran (Garis Singgung Persekutuan
Dalam Dua Lingkaran).
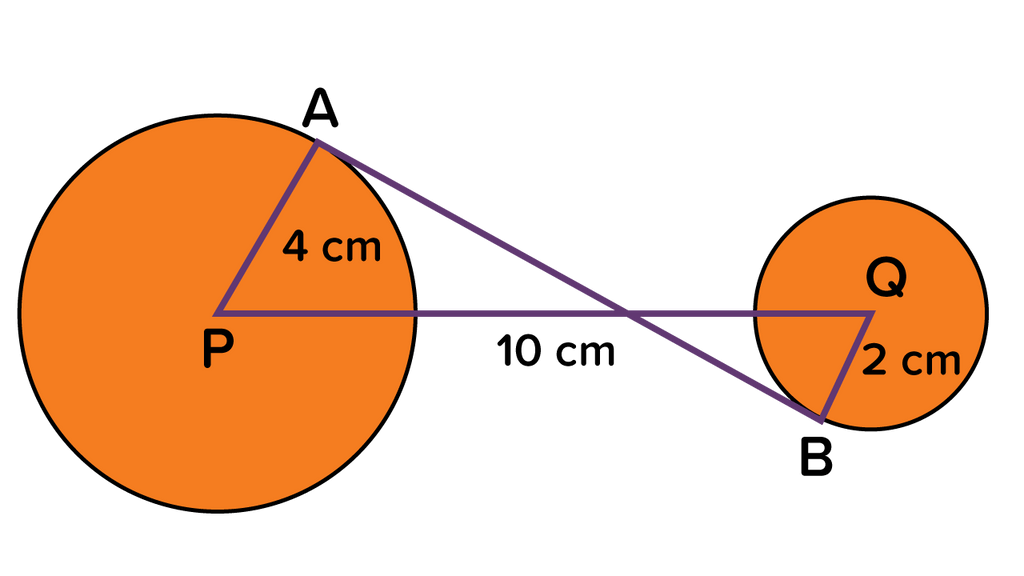
Garis Singgung Persekutuan Dalam Dua Lingkaran
Garis singgung
lingkaran adalah garis yang memotong lingkaran tepat di satu titik dan tegak
lurus dengan jari-jari yang melalui titik tersebut. Titik yang dimaksud adalah
titik singgung lingkaran. Ada dua jenis garis
singgung persekutuan dua lingkaran, yakni dalam dan luar. Garis singgung
persekutuan dalam adalah garis singgung persekutuan yang berada di bagian dalam
dari dua buah lingkaran. Rumus garis singgung persekutuan dalam dua lingkaran,
yakni:
d = Garis
singgung persekutuan dalam
P = Jarak kedua titik pusat lingkaran
R = Jari-jari
lingkaran besar
r = Jari-jari lingkaran kecil
Amati video berikut untuk memahami Garis Singgung Persekutuan Dalam Dua Lingkaran:
Ayo Berlatih!
1.Perhatikan gambar dibawah ini!
Panjang garis singgung persekutuan dalam dua lingkaran di atas adalah ... cm.2. Soal adapada buku cetak halaman 110 nomor 2.
Kelas 7
Perbandingan
Capaian Pembelajaran
Di akhir fase D, peserta didik dapat membaca, menuliskan, dan membandingkan bilangan bulat, bilangan rasional, bilangan desimal, bilangan berpangkat dan bilangan berpangkat tak sebenarnya, bilangan dengan menggunakan notasi ilmiah. Mereka dapat melakukan operasi aritmetika pada ragam bilangan tersebut dengan beberapa cara dan menggunakannya dalam menyelesaikan masalah Mereka dapat mengklasifikasi himpunan bilangan real dengan menggunakan diagram Venn. Mereka dapat memberikan estimasi/perkiraan hasil operasi aritmetika pada bilangan real dengan mengajukan alasan yang masuk akal (argumentasi). Mereka dapat menggunakan faktorisasi prima dan pengertian rasio (skala, proporsi, dan laju perubahan) dalam penyelesaian masalah.
Assalamualaikum Wr. Wb.
Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.
Selalu jaga kesehatan dan beribadah kepada Alloh SWT. Semoga selalu istiqomah dalam melaksanakan sholat dhuha dan sholat lima waktu.
Tujuan pembelajaran pada pertemuan hari ini adalah peserta didik dari peristiwa tertentu, dimungkinkan untuk dapat menggambar grafik perbandingan berbalik nilai
menggunakan koordinat dan memahami karakteristik grafik perbandingan
berbalik nilai dalam kaitannya dengan perubahan perbandingan berbalik nilai dan
cara menyelesaikannya.
Grafik Perbandingan Berbalik Nilai
Mari kita bahas materi pada buku cetak mulai halaman 145 tentang grafik perbandingan berbalik nilai.
Catatan penting
jika y adalah fungsi dari x dan hubungan antara variabel x dan y dinyatakan sebagai y = a/x, sehingga kita katakan bahwa y berbanding terbalik dengan x.
Perlu diperhatikan bahwa a adalah konstanta tidak 0, dan a disebut konstanta perbandingan.
Ayo berlatih!
Selesaikanlah di buku latihan soal pada buku cetak halaman 148.
![]()