Matematika
Kelas VIII
Kita akan mencoba membuat grafik dari masalah kenaikan harga permen ke dalam bidang Kartesius. Kita misalkan saja harga permen sebagai variabel y dan tahun sebagai variabel x. Kemudian, kita pilih selang tahun antara 2011-2019. Kita perkirakan harga permen di tahun 2011 seharga Rp150/buah dan setiap dua tahun sekali, harga permen meningkat secara tetap sebesar Rp25/buah. Jadi, kalo di tahun 2011 itu harga permen 150/buah, maka di tahun 2012 jadi 175/buah, setiap tahun selalu naik hingga mencapai harga Rp250/buah di tahun 2019.
Mengenal Persamaan Garis Lurus
Cara Menentukan Persamaan Garis Lurus
1. Jika diketahui gradien dan satu titik yang dilalui garis
Misalnya, suatu garis melalui sebuah titik, yaitu (x1, y1). Kamu dapat menentukan persamaan garis lurusnya dengan rumus:
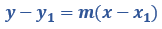
Contoh:
Tentukan persamaan garis yang bergradien 3 dan melalui titik (-2,-3)!
Penyelesaian:
Diketahui m = 3 dan (x1, y1) = (-2,-3). Sehingga,
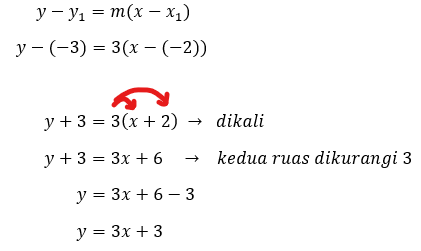
Jadi, persamaan garis lurusnya adalah y = 3x + 3.
2. Jika diketahui dua titik yang dilalui garis
Misalnya, suatu garis melalui dua buah titik, yaitu (x1, y1) dan (x2, y2). Kamu bisa menggunakan rumus di bawah ini untuk mengetahui persamaan garisnya.
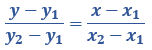
Ternyata, kalau kamu perhatikan, kondisi ini cocok untuk mencari persamaan garis lurus dari grafik kenaikan harga permen di atas. Coba yuk kita cari tahu persamaan garis lurusnya bersama-sama.
Pada gambar grafik kenaikan harga permen, diketahui kalau garis melalui beberapa titik. Misalnya, kita pilih dua titik dari beberapa titik tersebut, yaitu (x1, y1) = (2011, 150) dan (x2, y2) = (2019, 250). Sehingga,
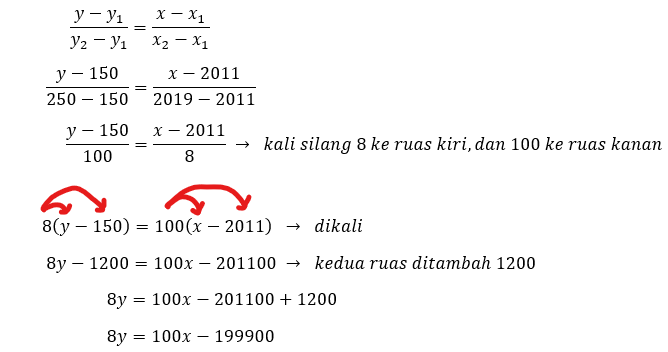
Jadi, persamaan garis lurus dari grafik kenaikan harga permen di atas adalah
8y = 100x – 199900.
Cara Menggambar Grafik dari Persamaan Garis Lurus
Contoh Soal:
Gambarlah grafik dari persamaan garis lurus y = 3x – 9!
1. Cari titik potong di sumbu x
Cara mencari titik potong pada sumbu-x adalah dengan membuat variabel y menjadi 0.

Jadi, saat y = 0, nilai x yang dihasilkan adalah 3. Sehingga, diperoleh titik potong di sumbu-x adalah (3,0).
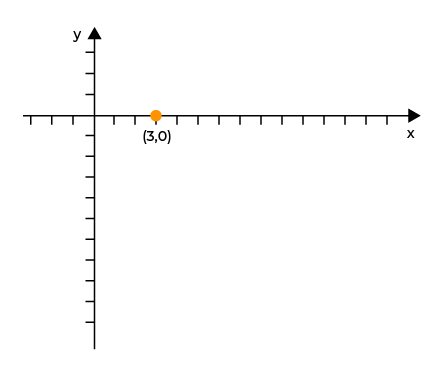
2. Cari titik potong di sumbu y
Tidak jauh berbeda dengan cara mencari titik potong pada sumbu-x, untuk mencari titik potong di sumbu-y, kita harus mengganti variabel x menjadi 0.

Jadi, saat x = 0, nilai y yang dihasilkan adalah -9. Sehingga, diperoleh titik potong di sumbu-y adalah (0,-9).
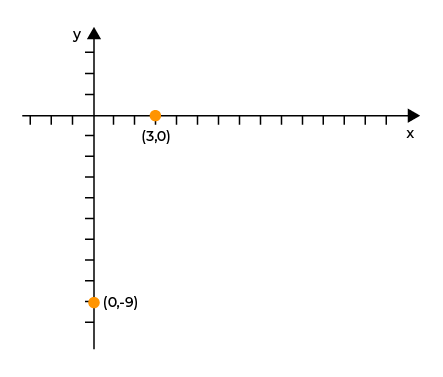
3. Gambar garis yang menghubungkan titik potong tersebut
Setelah diperoleh dua buah titik potongnya, kita bisa tarik garis lurus yang menghubungkan kedua titik potong tersebut. Sehingga, hasilnya akan seperti ini.
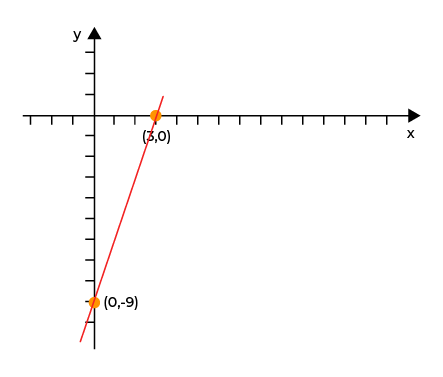


Tidak ada komentar:
Posting Komentar