Math

 Matematika

Kelas 9

Kesebangunan dan Kekongruenan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait perbandingan, peserta didik dapat menentukan kesebangunan dan kekongruenan segitiga-segitiga sebangun.

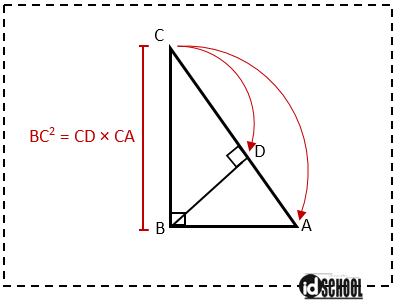
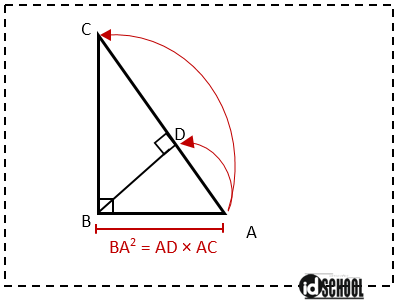
Rumus Kesebangunan pada Segitiga Siku-Siku

Dua buah segitiga yang sebangun, di mana kedua segitiga memiliki besar sudut – sudut yang bersesuaian sama besar. Didapatkan persamaan yang menyatakan perbandingan sisi – sisi yang bersesuaian dari kedua segitiga.

AB/PQ = BC/QR = AC/PR

Sudut A = Sudut P

Sudut B = Sudut Q

Sudut C = Sudut R

Contoh 

Perhatikan gambar!

Pada gambar tersebut, panjang KM adalah ….

Pembahasan:
Menghitung panjang KM:
KM2 = KN × KL
KM2 = 15 × (15 + 10)
KM2 = 15 × 25 = 375
KM = √375
Jadi, panjang KM adalah √375.

Kerjakan soal berikut

Perhatikan gambar berikut!

Panjang AC adalah ….

Kelas 7

Perbandingan

Assalamualaikum Wr. Wb.

Alhamdulillah hari ini dapat bertemu bersama untuk belajar matematika yang menyenangkan.

Tujuan pembelajaran pada pertemuan hari ini dengan diberikan sebuah permasalahan terkait perbandingan, peserta didik dapat menentukan perbandingan yang ekuivalen, menjelaskan perbandingan senilai (proporsi) sebagai suatu pernyataan dari dua perbandingan yang ekuivalen 5 : 2 = 10 : 4 dan membuat suatu perbandingan senilai untuk menentukan nilai x dalam 5 : 2 = 10 : x. 

Pengertian Perbandingan Senilai

Perbandingan senilai adalah perbandingan dua besaran yang digambarkan, apabila nilai suatu besaran meningkat, nilai besaran yang lain juga akan meningkat.

Sebaliknya, jika nilai suatu besaran menurun, nilai besaran yang lain juga ikut menurun. Contoh kejadian perbandingan senilai di antaranya adalah sebagai berikut.

Perbandingan antara jumlah barang dan harga barang.
Perbandingan antara jumlah tabungan dan waktu penyimpanan.
Perbandingan antara jarak tempuh kendaraan dan waktu tempuh.
Perbandingan antara jumlah makanan dan jumlah orang yang menghabiskan.
Perbandingan antara jumlah pekerja dan upah pembayaran yang dikeluarkan.

Sementara untuk rumus dari perbandingan senilai adalah a1/a2 = b1/b2.

Contoh

1. Jika diketahui bahwa A : B = 5 : 6. Jika pada nilai A = 20 maka berapakah nilai B?

Pembahasan:

A  : B = 5 : 6

20 : B = 5 : 6

5 x B = 20 x 6

   5 B = 120

      B = 120 : 5

      B = 24 

2. Sebuah konveksi dapat menjahit 150 potong pakaian selama 6 hari. Berapa banyak pakaian yang dapat dijahit selama 21 hari?

Pembahasan:

150 potong => 6 hari

x potong => 21 hari

Maka

150 potong/x Potong = 6 hari/21 hari

x potong = 150 potong. 21 hari/6 hari

x potong = 525 potong

Jadi selama 21 hari banyak pakaian yang dapat dijahit adalah 525 potong.

3. Jarak antara kota S dan kota M adalah 150 km, sedangkan jarak pada peta adalah 25 cm. Maka, berapa skala petanya? Skala = jarak pada peta/ jarak sebenarnya = 25 cm/ 150 km.

Pembahasan:

Skala = Jarak Peta : Jarak Sebenarnya

Jarak pada peta = 25 cm Jarak sebenarnya = 150 km = 15.000.000 cm

Diperoleh, skala = jarak pada peta/ jarak sebenarnya = 25 cm/ 150 km = 25 cm/ 15.000.000 cm = 1/ 600.000

Jadi, skala petanya adalah 1 : 600.000. Artinya, setiap jarak 1 cm pada peta mewakili 600.000 cm = 6 km pada keadaan sebenarnya.

Ayo berlatih!

Buku cetak halaman 40 soal no 7 dan 9.